
実在気体の状態方程式ができた!!!
これってどこまで使えるのだろうか?
記事①:pV=nRT 単位換算地獄 ~気体の状態方程式をPythonで! ep 1~
記事②:実在気体をPythonで解く~気体の状態方程式をPythonで! ep 2~
記事③:実在気体をPythonで解く(解決編)~気体の状態方程式をPythonで! ep 3~
前回、見事に実在気体の状態方程式を算出するプログラムを作ることが出来ました。
さて、今回はこの方程式がどこまで使えるのか?を検証してみたいと思います。
(2021年3月12日:学習開始21日目 PyQさんで学習中!)
気体をこれまで見てきましたが、空気といえば呼吸ですね。(ちょっと苦しい・・)
呼吸にまつわる曲で行きましょう。つながりが苦しいので、今回は2曲で行きます。
Maroon5の「Songs About Jane」から「Harder To Breathe」
The Prodigyの「The Fat Of The Land」から「Breathe」
どっちも超名盤やね!(どっちも公式YouTubeに飛びます。公式縛りでいきます。)
今回は、「水の実在気体の状態方程式」が完成します。
1.実在気体の状態方程式(前回おさらいと今回やりたい事)
前回、実際のデータから実在気体の状態方程式を出すプログラムを作りだしました。
詳細は前回記事参照としますが、かるくおさらいします。
ビリアル方程式を用いて状態方程式を出しました。式はこれです。
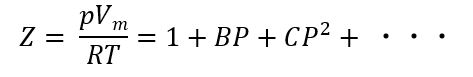
この式に水蒸気の5つの実測データをぶち込んで、B、C、D、E、Fの係数まで算出しました。
それぞれの値は、以下になりました。
B = -1.44102e-07
C = 1.24098e-13
D = -5.47952e-20
E = 8.89451e-27
F = -4.37502e-34ちなみにインプットしたデータはこちらのFNの高校物理さんの蒸気表のデータから抜粋さてていただきました。
| 温度(℃) | 圧力(MPa) | 比容積 (m3/kg) | |
| ① | 120 | 0.19853 | 0.8919 |
| ② | 170 | 0.7917 | 0.2428 |
| ③ | 220 | 2.318 | 0.08619 |
| ④ | 270 | 5.499 | 0.03564 |
| ⑤ | 320 | 11.274 | 0.015488 |
で、もともとインプットしたデータの温度と圧力から方程式を用いて比容積を計算したところ、実データー=計算した値とすることが出来たので、まずは妥当なものができたと思います。ここまでが前回。
そこで、今回は、この方程式がどこまで使えるのかを検証したいと思います。
2.検証方法
検証していきたいと思います。検証したいことは大きく2点です。
1つ目は、「インプットした5点以外でもつかえるのか?」
2つ目は、「もし5点以外で使えるのであれば、どの範囲まで使えるのか?」
ということです。
インプットした5点を見てみましょう。
今回使った5点は温度でいうと120℃~320℃の範囲の5点です。そこで今回やりたいのは、「120℃以下」「120℃~320℃の間」「320℃以上」の3つの領域でこの方程式を当てはめるとどうなるか?ということをやっていきます。
予想としては、「120℃~320℃の間」はそこそこ行けそうな気がしますが、「120℃以下」「320℃以上」は厳しいんじゃないかなと思います。
今回やることは単純で、できた式に実データを入れるだけなので、すぐできそうです。エクセルを使えば一発ですね。いやいや、エクセルでやってどうする!!もちろんpythonでやっていきます。
今回は5点のデータから算出しましたが、もっと汎用的なプログラム(2点でも50点でも当てはまるようなヤツ)でやりたいですね。
3.方程式の出力(とちょっとしたHomeWork)
今回の検証は、前回のプログラムに付け加えるというのではなく、独立したものにしたいと思っています。そうなると、前回の結果を今回作成するプログラムに持ってくる必要があります。
では、前回の結果とは何か?それは、B~Fの値ですね。
これを前回のプログラムからcsvでアウトプットして、今回のプログラムではcsvをオープンするという感じでやっていきます。
まずは、前回の結果のアウトプットからやっていきますが、その前に一つやり残したことがあります。
前回のプログラムでは、係数にB~Zをおきました。その結果、インプットする値が25以上になるとうまく動かないはずです(やってみていませんが・・)。
そこで、係数をアルファベットではなくNo.1、No.2のように数字にすることで、どれだけインプットしても大丈夫なプログラムにしたいと思います。
本題のcsv形式の出力ですが、いつも隣にITのお仕事さんのページPythonでcsvファイルにデータを書き込みをする基本中の基本を参考にさせていただきました。ありがとうございます!
これらを踏まえて、前回のプログラムを修正しました。
R = 8.314462 #気体定数[J/K・mol]
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/xxxx/yyyy/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dic
def solve_renritsu(con_dat_dic):#con_dat_dicを入れれば係数が変える関数
from numpy.linalg import solve #numpyのsolveをインポート
right_list =[]#右辺の空リスト
left_list =[]#左辺の空リスト
for num, st_list in con_dat_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
z = (pres*volu) / (R*temp) #Z=PV/RT
right = z-1 # right = pv/rt - 1
right_list.append(right)#right_list=[z1-1,z2-1・・・]
left = []#1データの左辺(pB+p^2C+p^3D・・・)
for p_num in list(range(1, 1+len(con_dat_dic))):#p_num = 1~データ
left.append(pres**p_num) #left = [p, p^2, p^3 ・・・]
left_list.append(left) #left_list = [[left1], [left2]・・・]
solve_list = solve(left_list, right_list)#連立方程式の解
for keisu_no in list(range(1, 1+len(con_dat_dic))):
sol = solve_list[keisu_no-1]
print(f'係数No.{keisu_no} = {sol:.5e} ')
return(solve_list)
def kensyou(c_dat_dic, s_list):#c_dat_dicとs_listを入れれば検証できる関数
for num_2, st_list_2 in c_dat_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
z_2 = 1 #Z_2 = 1 + BP + BP^2 +・・・
for y in list(range(0, len(c_dat_dic))): #y = 0~データ数-1
z_2 += s_list[y]*(pres**(y+1)) #Z_2にs_list[0]*p**1, s_list[1]*p**2・・・を加える。
Vb = (z_2)*(R*temp)/pres #ビリアルの状態方程式から計算
print(f'{num_2} : 実データのVm:{volu:.5f} 理想気体のVm:{vid:.5f} ビリアルの状態方程式から求まるのVm:{Vb:.5f}')
data_dic = list_input()
solve_keisu = solve_renritsu(data_dic)
print(solve_keisu)
kensyou(data_dic, solve_keisu)
import csv
with open('C:/Users/xxxx/yyyy/steam_solve.csv', 'w', encoding = 'utf-8') as f:
writer = csv.writer(f)
writer.writerow(solve_keisu)変更点は大きく3つです。
1点は、はじめのアルファベットのリストは使用しないので削除しました。
2点目はdef solve_renritsu(con_dat_dic):の中を変えています。係数No. 1 = XXXXとなるように書き換えています。
3点目が最後のデータの出力です。steam_solve.csvというファイルを作り出力するようにしています。ここで注意がいるのが、csv形式で出力するには、csvというモジュールをインポートする必要があるということです。ここではcsv形式のファイルで、solve_keisu、つまり係数のリストを出力しています。
結果、以下のようになりました。
係数No.1 = -1.44102e-07
係数No.2 = 1.24098e-13
係数No.3 = -5.47952e-20
係数No.4 = 8.89451e-27
係数No.5 = -4.37502e-34
[-1.44101867e-07 1.24097733e-13 -5.47952452e-20 8.89450881e-27
-4.37502122e-34]
0 : 実データのVm:0.01607 理想気体のVm:0.01647 ビリアルの状態方程式から求まるのVm:0.01607
1 : 実データのVm:0.00437 理想気体のVm:0.00465 ビリアルの状態方程式から求まるのVm:0.00437
2 : 実データのVm:0.00155 理想気体のVm:0.00177 ビリアルの状態方程式から求まるのVm:0.00155
3 : 実データのVm:0.00064 理想気体のVm:0.00082 ビリアルの状態方程式から求まるのVm:0.00064
4 : 実データのVm:0.00028 理想気体のVm:0.00044 ビリアルの状態方程式から求まるのVm:0.00028うまく行っていますね。真ん中あたりにあるリストがsolve_keisuで、あえてprintしました。これがcsv形式のファイルで出力されているはずです。
そこで該当のフォルダを見ると、確かに「steam_solve.csv」が作られていました。
中身をメモ帳でひらくと、
-1.4410186675280982e-07,1.2409773320571073e-13,-5.479524524577397e-20,8.894508808447889e-27,-4.37502122322995e-34
となっており、係数の値が「, 」で区切られています。おそらく成功です!!
では、今作成したcsvファイルを使って、検証に取り掛かりましょう!
4.フローチャートをつくろう
さて、新しいプログラムに入る前にフローチャートを作成します。
今回は当初の予定どおり、単純ですね。サクッと作っていきましょう。
5.プログラムを書こう
まず、係数データのインプットから行きます。
どのような感じでインプットされるか分からないので、まずはprintしてみます。プログラムはこんな感じです。ファイルの位置はsteam_solve.csvを作ったところです。
def solve_input():
with open('C:/Users/xxxx/yyyy/steam_solve.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_solve.csvを開く
print(row)
solve_input()結果はこんなかんじになりました。
-1.4410186675280982e-07,1.2409773320571073e-13,-5.479524524577397e-20,8.894508808447889e-27,-4.37502122322995e-34・・・なんか違和感。まずデータは「,」で区切られていますが、ひと塊になっています。
それと、データのあとにブランクがたくさんあります。
ちょっとプログラムは修正しましょう。こんな感じです。strip()で空白を除外しています。split(‘,’)で値を分割しています。
def solve_input():
with open('C:/Users/xxxx/yyyy/steam_solve.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_solve.csvを開く
print(row.strip().split(','))
solve_input()で、結果はこう。
['-1.4410186675280982e-07', '1.2409773320571073e-13', '-5.479524524577397e-20', '8.894508808447889e-27', '-4.37502122322995e-34']
['']なんか余計なやつがおる![”]こいつですよ。こいつ。removeでとれるかな?
もう一つ修正すべき点があります。前半のリスト値が文字列(str)になっています。
def solve_input():
solve_list = []
with open('C:/Users/xxxx/yyyy/steam_solve.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_solve.csvを開く
solve_list += row.strip().split(',')
solve_list.remove('')
print(solve_list)
solve_input()結果はこうです。
['-1.4410186675280982e-07', '1.2409773320571073e-13', '-5.479524524577397e-20', '8.894508808447889e-27', '-4.37502122322995e-34']文字列になっているのは解決していませんが、ひとつずつデータを出すときにfloatを使えば行けそうなので、まあ良しとします。(ここまでサッと書きましたが、結構何度か修正しました。)
print(solve_list)をreturn solve_listとしておいて、係数データのインプットはこれで行きましょう。
つぎは、実在気体のデータのインプットです。
FNの高校物理さんの蒸気表のデータから抽出させてもらいました。使ったのはこのデータです。
| 温度(℃) | 圧力(MPa) | 比容積 (m3/kg) | |
| ① | 80 | 0.04739 | 3.407 |
| ② | 90 | 0.07014 | 2.361 |
| ③ | 100 | 0.10135 | 1.6729 |
| ④ | 150 | 0.4758 | 0.3928 |
| ⑤ | 200 | 1.5538 | 0.12736 |
| ⑥ | 300 | 8.581 | 0.02167 |
| ⑦ | 340 | 14.586 | 0.010797 |
| ⑧ | 360 | 18.651 | 0.006945 |
| ⑨ | 370 | 21.03 | 0.004925 |
このままだと、Pythonにインプットすることができないので、上端の「温度」等と左端の番号と削ってcsv形式のファイルにしました。
(前々回同様にエクセル使っています、たぶんweスクレイビングとかできればもっとうまくやれるんでしょうね。ちょっとまだ早いかな)
80,0.04739,3.407
90,0.07014,2.361
100,0.10135,1.6729
150,0.4758,0.3928
200,1.5538,0.12736
300,8.581,0.02167
340,14.586,0.010797
360,18.651,0.006945
370,21.03,0.004925
これを「steam_kensyo.csv」というファイル名で作成しておきます。
次はこのデータのインプットですが、前回、前々回に作ったのをファイル名以外はそのまま流用できます。プログラムはこんな感じです。
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/xxxx/yyyy/steam_kensyo.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_kensyo.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dicここだけ実行すると、結果はこうなります。
{0: [353.15, 47390.0, 0.06137805896000001], 1: [363.15, 70140.0, 0.042534076080000004], 2: [373.15, 101350.0, 0.030137761912000006], 3: [423.15, 475800.0, 0.007076401984000001], 4: [473.15, 1553800.0, 0.0022944260608], 5: [573.15, 8581000.0, 0.00039039111759999997], 6: [613.15, 14586000.0, 0.00019451097816], 7: [633.15, 18651000.0, 0.0001251161196], 8: [643.15, 21030000.0, 8.872525399999999e-05]}実在気体のデータはOKですね。
次は、方程式の作成にいきましょう。
ここは、過去にやったものとほぼ同じなので、Vmの計算まで一気にいきます。これで完了なので、今までもプログラムも全部合算して、最終こうなりました。
R = 8.314462 #気体定数[J/K・mol]
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/xxxx/yyyy/steam_kensyo.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_kensyo.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dic
def solve_input():
solve_list = []
with open('C:/Users/xxxx/yyyy/steam_solve.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam_solve.csvを開く
solve_list += row.strip().split(',')
solve_list.remove('')
return solve_list
def kensyou(c_dat_dic, s_list):#c_dat_dicとs_listを入れれば検証できる関数
for num_2, st_list_2 in c_dat_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
z = 1 #Z_2 = 1 + BP + BP^2 +・・・
for y in list(range(0, len(s_list))): #y = 0~係数の数-1
z += float(s_list[y])*(pres**(y+1)) #Z_2にs_list[0]*p**1, s_list[1]*p**2・・・を加える。
Vb = z*(R*temp)/pres #ビリアルの状態方程式から計算
print(f'{num_2} :T = {temp}K 実データのVm:{volu:.5f} 理想気体のVm:{vid:.5f} ビリアルの状態方程式から求まるのVm:{Vb:.5f}')
data_dic = list_input()
solve_keisu = solve_input()
kensyou(data_dic, solve_keisu)実行した結果はこうなりました!
0 :T = 353.15K 実データのVm:0.06138 理想気体のVm:0.06196 ビリアルの状態方程式から求まるのVm:0.06155
1 :T = 363.15K 実データのVm:0.04253 理想気体のVm:0.04305 ビリアルの状態方程式から求まるのVm:0.04264
2 :T = 373.15K 実データのVm:0.03014 理想気体のVm:0.03061 ビリアルの状態方程式から求まるのVm:0.03020
3 :T = 423.15K 実データのVm:0.00708 理想気体のVm:0.00739 ビリアルの状態方程式から求まるのVm:0.00705
4 :T = 473.15K 実データのVm:0.00229 理想気体のVm:0.00253 ビリアルの状態方程式から求まるのVm:0.00232
5 :T = 573.15K 実データのVm:0.00039 理想気体のVm:0.00056 ビリアルの状態方程式から求まるのVm:0.00119
6 :T = 613.15K 実データのVm:0.00019 理想気体のVm:0.00035 ビリアルの状態方程式から求まるのVm:-0.01083
7 :T = 633.15K 実データのVm:0.00013 理想気体のVm:0.00028 ビリアルの状態方程式から求まるのVm:-0.06354
8 :T = 643.15K 実データのVm:0.00009 理想気体のVm:0.00025 ビリアルの状態方程式から求まるのVm:-0.13138ここで0~2が80℃~100℃で、「120℃以下」
3~5が150℃~300℃で「120℃~320℃(係数算出に使った範囲)」
6~9が340℃~370℃で「320℃以上」
これで分かるのは、温度の低い領域(0~2)では、十分適応できそうです。これは、意外でした。100℃で常圧下では水から水蒸気と大きな状態変化があるので、120℃以上の値から算出した値は使えないと思っていましたが大丈夫なんですね。
3~5は係数算出範囲内のデータなのでおおむね行けるのですが、5の320℃が結構ズレています。なんなら、理想気体のデータの方が実データに近いです。
6~9は全然ダメでマイナスになってしまっています。高温領域はズレが大きくなってしまうようです。
では、下の温度はどこまでいけるのでしょうか?蒸気表の下限温度(0.01℃)とその上の5℃でやってみるとこうなりました。
0 :T = 273.15999999999997K 実データのVm:3.71367 理想気体のVm:3.71533 ビリアルの状態方程式から求まるのVm:3.71500
1 :T = 278.15K 実データのVm:2.65041 理想気体のVm:2.65184 ビリアルの状態方程式から求まるのVm:2.65150なぜか0.01℃の際の温度がおかしな値になりますが、これは内部の計算上の誤差のようです。
で、結果的に0.01℃でも適応できます。かなり意外でした。こんなんほぼ氷ですからね。
こうなってくると、高温側もうまく方程式に乗せたいですね。
大量にデータをぶち込んで方程式を作ってみます。
今回、検証に使ったデータ+高温のデータを係数算出のインプットとしてやってみます。
使ったデータは以下です。低温~高温まで網羅しています。プログラムは冒頭に作ったものです。
| 温度(℃) | 圧力(MPa) | 比容積 (m3/kg) | |
| ① | 0.01 | 0.0006113 | 206.14 |
| ② | 5 | 0.0008721 | 147.12 |
| ③ | 80 | 0.04739 | 3.407 |
| ④ | 90 | 0.07014 | 2.361 |
| ⑤ | 100 | 0.10135 | 1.6729 |
| ⑥ | 150 | 0.4758 | 0.3928 |
| ⑦ | 200 | 1.5538 | 0.12736 |
| ⑧ | 300 | 8.581 | 0.02167 |
| ⑨ | 315 | 10.547 | 0.016867 |
| ⑩ | 320 | 11.274 | 0.015488 |
| ⑪ | 330 | 12.845 | 0.012996 |
| ⑫ | 340 | 14.586 | 0.010797 |
| ⑬ | 360 | 18.651 | 0.006945 |
| ⑭ | 370 | 21.03 | 0.004925 |
結果、こうなりました。
14個のデータから14係数が算出され、14個のアウトプットが出ているのでプログラムはうまく働いています。
一方で高温のデータはあまりよくないです。中にはマイナスの値をとっているものもあります。
係数が多すぎるとどうなるか?たとえば係数No.14の項は「-8.12547e-88 x P14」という値になります。
最後のデータのPは21030000Paですので、P14はとてつもなく大きな値となります。
「とてつもなく小さい値 x とてつもなく大きい値」となるので、どちらも小数点以下の値が拡大されて結果に反映されます。
係数を増やしすぎてはいけないということです。
いままでの結果から、低温側は結構合うっぽいので、高温側だけで係数計算をしてみます。
上の蒸気圧の表から高温の⑩320℃~⑭370℃だけを使って計算してみました。
結果はこうなりました。
係数No.1 = -6.77539e-08
係数No.2 = 7.97717e-15
係数No.3 = -7.05148e-22
係数No.4 = 3.06603e-29
係数No.5 = -5.33089e-37
[-6.77539249e-08 7.97716545e-15 -7.05147672e-22 3.06603149e-29
-5.33089497e-37]
0 : 実データのVm:0.00028 理想気体のVm:0.00044 ビリアルの状態方程式から求まるのVm:0.00028
1 : 実データのVm:0.00023 理想気体のVm:0.00039 ビリアルの状態方程式から求まるのVm:0.00023
2 : 実データのVm:0.00019 理想気体のVm:0.00035 ビリアルの状態方程式から求まるのVm:0.00019
3 : 実データのVm:0.00013 理想気体のVm:0.00028 ビリアルの状態方程式から求まるのVm:0.00013
4 : 実データのVm:0.00009 理想気体のVm:0.00025 ビリアルの状態方程式から求まるのVm:0.00009うまく行きました。やはり係数はむやみに増やしてはいけないということです。
では、これを使って低温側でも当てはまるかを検証してみます。
検証には蒸気圧のデータ14点すべてをぶち込みました。
0 :T = 273.15999999999997K 実データのVm:3.71367 理想気体のVm:3.71533 ビリアルの状態方程式から求まるのVm:3.71517
1 :T = 278.15K 実データのVm:2.65041 理想気体のVm:2.65184 ビリアルの状態方程式から求まるのVm:2.65168
2 :T = 283.15K 実データのVm:1.91647 理想気体のVm:1.91776 ビリアルの状態方程式から求まるのVm:1.91760
3 :T = 353.15K 実データのVm:0.06138 理想気体のVm:0.06196 ビリアルの状態方程式から求まるのVm:0.06176
4 :T = 363.15K 実データのVm:0.04253 理想気体のVm:0.04305 ビリアルの状態方程式から求まるのVm:0.04285
5 :T = 373.15K 実データのVm:0.03014 理想気体のVm:0.03061 ビリアルの状態方程式から求まるのVm:0.03040
6 :T = 423.15K 実データのVm:0.00708 理想気体のVm:0.00739 ビリアルの状態方程式から求まるのVm:0.00717
7 :T = 473.15K 実データのVm:0.00229 理想気体のVm:0.00253 ビリアルの状態方程式から求まるのVm:0.00231
8 :T = 573.15K 実データのVm:0.00039 理想気体のVm:0.00056 ビリアルの状態方程式から求まるのVm:0.00039
9 :T = 588.15K 実データのVm:0.00030 理想気体のVm:0.00046 ビリアルの状態方程式から求まるのVm:0.00030
10 :T = 593.15K 実データのVm:0.00028 理想気体のVm:0.00044 ビリアルの状態方程式から求まるのVm:0.00028
11 :T = 603.15K 実データのVm:0.00023 理想気体のVm:0.00039 ビリアルの状態方程式から求まるのVm:0.00023
12 :T = 613.15K 実データのVm:0.00019 理想気体のVm:0.00035 ビリアルの状態方程式から求まるのVm:0.00019
13 :T = 633.15K 実データのVm:0.00013 理想気体のVm:0.00028 ビリアルの状態方程式から求まるのVm:0.00013
14 :T = 643.15K 実データのVm:0.00009 理想気体のVm:0.00025 ビリアルの状態方程式から求まるのVm:0.00009おーーーおーーーーー!
ほぼ全温度域に渡って、実データのVmと方程式から求まるVmが非常に近い値を取っています。
水(水蒸気)は374℃を超えると超臨界水という状態になることが知られています。
超臨界は詳しく説明できませんが、とにかくいわゆる水蒸気ではないヤバい状態になる、ということです。
今回はその直前の370℃まで対応できており、低温は氷となる直前の0.05℃まで対応しています。いま、ここに水の実在気体の状態方程式が完成しました。

(※素人が遊び半分どころか遊び全部で作っただけなので、100%責任は持ちません。)
いや~長かった~。状態方程式はもう満足したので、これで終わりです。
Fin.
PyQさんで勉強中!





コメント