
前回は理想気体の状態方程式で「単位換算から計算まで全部乗せマシーン」を作った。
今回は、実在気体へ挑戦してみよう!
記事①:pV=nRT 単位換算地獄 ~気体の状態方程式をPythonで! ep 1~
前回は、単位換算をしなくても持っている値をどんどん打ち込めば、好きな単位で答えを返してくれる計算機を作ってみました。
やってみたものの、正直な感想として、Exelでよくない?って感じでした。
結構な労力を使った割に、出来上がったものがたいしたことないというか・・・
ま、元のコンセプト「pythonの無駄使い」を発揮したとも言えるような、言えないような。
前回の失敗(失敗って言っちゃった)の原因は、「電卓でも出せる単純計算をやらせたこと」にあるように思います。
では、単純計算ですぐにできなさそうなこと、というわけで実在気体と戦いましょう!
(2021年3月6日:学習開始15日目 PyQさんで学習中!)
今回は、Redioheadさんの歴史的大名盤「OK Computer」から「Airbag」(Airだけに!)とともに進めていきましょう。(曲名から公式YouTubeに飛びます。)
先に言っておきますが、今回は大爆死します。
1.実在気体とどう戦うか?
実在気体とは何でしょうか?読んで字のごとく、「実在」の「気体」です。
あえてこのような言い方をするのは、前回取り扱った「理想気体」が実際とはかけ離れているからです。
過去、多くの科学者がこの「実在気体」の状態方程式を明らかにすべく様々な検討がなされてきました。(参照:wikipedia「実在気体」、技術情報館さんの化 学 第三部:物質の状態と変化)
詳細は割愛しますが、様々な考えのもと、理想気体の状態方程式をベースに補正をかけていった訳です。
今回、いくつかある実在気体の状態方程式のうち、「ビリアル方程式」をベースにやって見ようと思います。ビリアル方程式は、以下のような方程式です。
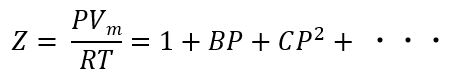
右側の式の1項目で終われば理想気体、それ以降の項で補正をかけていくという考え方です。
ちなみにVmはモル体積で、1molあたりの体積です。つまりn=1として考えればよいですね。
この式に注目した理由は、ずばり、「式が無限に続く形になっているから」です。
他の式は、物理的な意味を考えたうえで、式が閉じた形になっています(参照:ファンデルワールスの状態方程式)。この場合、1つ、または2つの状態が与えられれば、補正項が決まるという事になります。だったら、プログラミングを使うまでもなく計算できますよね?
ところが、ビリアルの式は無限に補正していく形式になっているので、いくつかの状態をインプットして補正をかけ続けると、限りなく実態に近づいていくはずです。
繰り返しの計算ならば、プログラミングでいい感じになると思いませんか?
2.ビリアル方程式を考えよう!
さて、ビリアル方程式を取り扱うと決めたわけですが、どのようにやっていくかを考えましょう!
「ビリアル方程式をキチンと解く」ということではなく、「この式をベースに補正をかける」という考えで進めます(物理学者の皆様、すみません)。
まず、式をよく見てみましょう。
補正項は1+ BP+CP2 +・・・となっています。ではこの先はどうなってくのでしょうか?
まず、アルファベット順にA、B、C、と来てAP0(=1)、BP1 、CP2となっているのが分かります。では、アルファベットがSならどうでしょうか?Sはアルファベット順で19ですので、SP19となります。
では、さらに続くとどうなるか?実際は記号だけの問題なので、どこまででも続けることはできますが、さすがにそれは扱いにくいです。ですので、今回はA~Z(26番目)までの式として取り扱いたいと思います。式は以下のようになります。
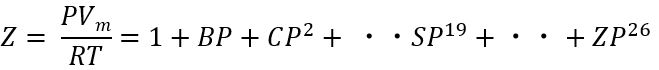
これでB ~ Zまで求めればよいということになります。
次は、どのようにB ~ Zを求めるかを考えましょう。
以下の2つの考えのもと、進めていきたいと思います。
①:補正項は少ない方がよい。
②:前の補正項(Pの乗数が少ない項)を優先とする。
この考えから行くと、まずB → C → D、、、と計算していくことになります。
それでどこで止めるかというと、「アルファベットの値がほぼ0になったところ」と考えればよいと思われます。
だんだん具体的な計算方法が定まってきました。
手順①:まず、C以降は無視します。
手順②:いくつかの実状態(p、Vm、T)をインプットするとそれぞれの状態でBが求まります。
手順③:すべての状態でBがほぼ0であれば計算終了。そうでなければ計算続行
手順④:いくつか算出されたBの平均値をとる。
手順⑤:Bの平均値をBと設定する。
手順⑥:D以降を無視してCを計算、以下繰り返し。
上のような考えでどうでしょうか?なんか行けそうな気がします。
この考えの元、B、C、Sを求める式は以下のようになります。
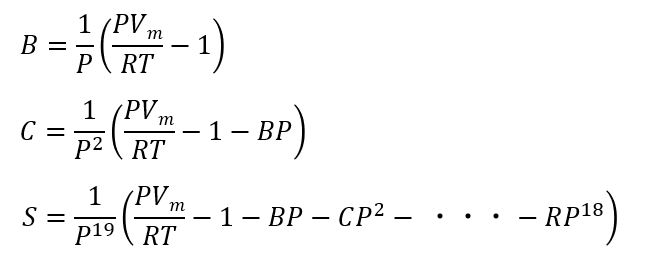
ポイントは、下にいく度に①1/pがかけられる ②カッコ中で特定の値(BP、CP2・・)が引かれる。もう少し考えてみましょう。まず、事前に次の辞書型のデータを考えます。
dic = {1:B, 2:C, ・・・n:(n+1番目のab), n+1:(n+2番目のab),・・,27:Z]
(※ab =アルファベット)

これを活用して、うまくループさせれば行けそうな気がします。
3.作戦会議
フローチャートで書いていきましょう。
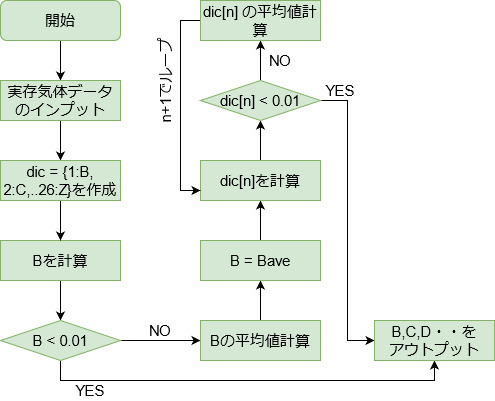
どうでしょうか。ちょっと不安ですが、先に進めてみます。
(※後で気づきましたが、dic ={1:B, 25:Z}です。)
ところで、インプットするデータですが、こちらのFNの高校物理さんの蒸気表のデータを使わせていただきました。これから5点程度データを使用して計算してみます。
では、プログラムを書いていきます。
4.プログラムを書いてみよう
まずは、データのインプットです。
先ほどの蒸気表のデータから、5点ピックアップさせていただきました。
| 温度(℃) | 圧力(MPa) | 比容積 (m3/kg) | |
| ① | 120 | 0.19853 | 0.8919 |
| ② | 170 | 0.7917 | 0.2428 |
| ③ | 220 | 2.318 | 0.08619 |
| ④ | 270 | 5.499 | 0.03564 |
| ⑤ | 320 | 11.274 | 0.015488 |
このままだと、Pythonにインプットすることができないので、上端の「温度」等と左端の番号と削ってcsv形式のファイルにしました。(反則気味ですが、エクセルでやりました。)
120,0.19853,0.8919
170,0.7917,0.2428
220,2.318,0.08619
270,5.499,0.03564
320,11.274,0.015488
これを「steam.csv」というファイル名で作成しておきます。これで事前準備は完了です。
では「インプットするプログラム」から書いていきます。
まずは、インプットできるかどうかを確認してみます。
なお、’C:/Users/XXXX/YYYY/steam.csv’は、それぞれsteam.csvを格納しているフォルダにより異なります。
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
print(row)結果は以下の通りです。
120,0.19853,0.8919
170,0.7917,0.2428
220,2.318,0.08619
270,5.499,0.03564
320,11.274,0.015488
読み込ませることはできました。
このままでは、使いづらいので「改行をなくし」「リスト形式で読み込ませたい」と思います。
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
print(row.strip().split(','))#改行なくし #','で区切る出力はこんな感じです。
['120', '0.19853', '0.8919']
['170', '0.7917', '0.2428']
['220', '2.318', '0.08619']
['270', '5.499', '0.03564']
['320', '11.274', '0.015488']ポイントは3つ、
①1行ごとにリストになっている。
②各値が文字列(str形式)になっている。
③各値が「,」で区切られている。
という点に留意しておく必要がありそうです。
このデータはすぐに使うわけではないので、いったんおいておきます。
続いて、辞書形式のデータで{1:B, 2:C,・・・25:Z}を入れていきます。
頑張ってて手入力してもいいのですが、プログラムでできないはずがないので、やり方を考えてみます。
1~25までをいれていく方法は、renge(1,26)が使えました。これの英語大文字verがあればよさそうです。
調べてみると、以下のような書き方で出力できるようです。
print([chr(ord('A')+i) for i in range(26)]) #大文字アルファベット結果は以下のようになります。
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']これは、何をしているのでしょうか?考えてみます。
まずord関数。これは、文字列を数字に読み替えるようです。
そもそも、pythonでは、それぞれの文字に番号が割り振られているそうです。(だから、あいうえお順でもsortできる!)それを読み出すのがord関数です。
つづいて、chr関数。こちらは、ordの逆で、数字を対応する文字列に変換するようです。
つまりここで行われいるのは、[A→A番号→A, A番号+1→B, ・・・A番号+25→Z]というとですね。
これらをうまく使えば、{1:B, 2:C,・・・25:Z}が作れそうです。
やってみましょう。forで1~25回からの辞書に1:B、2:Cと加えていけば良さそうです。
出来上がりを見たいので、最後にprintしてみます。
num_ab_dic = {} #数字:アルファベット辞書作成
for dic_num in range(1,26):
num_ab_dic[dic_num] = chr(ord('B')- 1 + dic_num)
print(num_ab_dic)結果は以下です。
{1: 'B', 2: 'C', 3: 'D', 4: 'E', 5: 'F', 6: 'G', 7: 'H', 8: 'I', 9: 'J', 10: 'K', 11: 'L', 12: 'M', 13: 'N', 14: 'O', 15: 'P', 16: 'Q', 17: 'R', 18: 'S', 19: 'T', 20: 'U', 21: 'V', 22: 'W', 23: 'X', 24: 'Y', 25: 'Z'}かなりうまくいきました。使うときはprintは不要ですので、消しておきましょう。
つぎは、「Bの計算」です。
ここでは、まず具体的にBを算出してみますが、最終的に上の辞書型データでループをさせていきたいので、その点を踏まえて考えていきます。
さらにここから、インプットした蒸気圧のデータで計算を回す必要があります。
プログラムに移る前に少し整理しておきます。
やりたいのは、下の計算です。
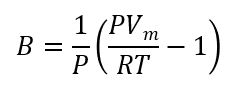
インプットするデータは[‘120’, ‘0.19853’, ‘0.8919’]のようになっています。
これを[‘list1’, ‘list2’, ‘list3’]とします。計算のためには文字列→数字変換が必要です。
それぞれの内容は、[‘温度(℃)’, ‘圧力(kPa)’, ‘比容積 (m3/kg)’]ということになっています。
これらのデータは、[T(K), P(Pa), Vm(m3/mol)]に変換してやる必要があります。
今回は水蒸気、つまりH2Oですので分子量M=18.01528 g/mol です。
比容積 (m3/kg)*0.001(kg/g)*18.01528 (g/mol) = Vm(m3/mol)
それぞれやってみると、
[float(‘list1’) + 273.15, float(‘list2’)*1000, float(‘list3’)*0.001*18.01528]
で計算ができる形式になります。簡単のためにこのリストは[list_t, list_p, list_v]と書きましょう。
(前回つくったプログラムをガン無視してる・・)
ここまでを折り込んで、Bの式を書いてみましょう。
B = 1/list_p * (((list_p * list_v)/(R * list_t))-1)
このような計算をインプットするデータごとに繰り返すので、Bは5回計算できます。
B1、B2、B3、B4、B5が出てくるわけです。これらを平均すればBの平均値Baveが計算できます。
ここまでをプログラムで書いてみましょう。データインプットのところで、1行ずつ処理する形(for row in f:)をすでにとっているので、そこに加える形でやってみましょう。
ついでに、検証のため理想気体の状態方程式から算出した結果と比べてみましょう。
R = 8.314462 #気体定数[J/K・mol]
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
B = (1/list_p) * (((list_p * list_v)/(R * list_t))- 1) #Bの計算
vid= (R*list_t)/list_p #理想気体として計算
Vb = (1+ B*list_p)*(R*list_t)/list_p #Bを入れて計算
print(f'B = {B}, 実データのVm:{list_v:.5f}, 理想気体のVm:{vid:.5f}, Bを入れて計算:{Vb:.5f}')結果は以下の通りです。
B = -1.2155553345828597e-07, 実データのVm:0.01607, 理想気体のVm:0.01647, Bを入れて計算:0.01607
B = -7.595691017498863e-08, 実データのVm:0.00437, 理想気体のVm:0.00465, Bを入れて計算:0.00437
B = -5.2715626189823836e-08, 実データのVm:0.00155, 理想気体のVm:0.00177, Bを入れて計算:0.00155
B = -3.967574209794954e-08, 実データのVm:0.00064, 理想気体のVm:0.00082, Bを入れて計算:0.00064
B = -3.2122955574469773e-08, 実データのVm:0.00028, 理想気体のVm:0.00044, Bを入れて計算:0.00028うまく行きました!
いくつか気づく点があります。
①:Bの値はそれぞれ思っていたよりかなり小さい
②:理想気体の方程式はまあまあイケてる。
③:Bを入れて計算すると、実データと全く同じ値になる。
まず、①ですが、最初の想定ではB<0.01としましたが、すでにクリアしています。もっと小さい値で中止とした方がよさそうです。
②については、思った以上に近い値です。
③については、現時点では、それぞれの入力値に対してBを計算し、それぞれ別のBの値を入れて算出しているので、絶対に実データと一致します。
ここで、Bを共通の値(Bの平均値)を入れて計算するとどうなるのでしょうか?
Bを平均して(=Bave)、Bに代入して計算したいところですが、Bを平均するにはBを一度すべて計算する必要があります。
ということは、
「for構文でデータを開いて変換、Bを5つ計算」→Baveを計算→「for構文でデータを開いて変換、Baveを代入して計算」をする必要があります。
これをC、D、・・・とやっていくことになるので、共通する部分はdefで関数を定義した方がよさそうです。まずはここからやりましょう。
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dic
data_dic = list_input()
print(data_dic)結果こうなります。
{0: [393.15, 198.53, 0.016067828232000002], 1: [443.15, 791.6999999999999, 0.004374109984], 2: [493.15, 2318.0, {0: [393.15, 198530.0, 0.016067828232000002], 1: [443.15, 791700.0, 0.004374109984], 2: [493.15, 2318000.0, 0.0015527369832], 3: [543.15, 5499000.0, 0.0006420645791999999], 4: [593.15, 11274000.0, 0.00027902065664]}出力したデータが長いですが、要は、データ5つに対して0~4の番号をキーとして、[list_t, list_p, list_v]のデータリストを値として持っている辞書型のデータに置き換えました。
これを活用して、Bの計算とBの代入、再計算をやってみました。
プログラムは以下です。
R = 8.314462 #気体定数[J/K・mol]
def list_input():
list_num = 0 #データ数カウント
~~~~略~~~~
return conv_data_dic
data_dic = list_input()
B_total = 0
for num, st_list in data_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
B = (1/pres) * (((pres * volu)/(R * temp))- 1) #Bの計算
B_total += B
B_ave = B_total/len(data_dic)
for num, st_list_2 in data_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
Vb = (1+ B_ave*pres)*(R*temp)/pres #Bを入れて計算
print(f'B = {B:.5e}, 実データのVm:{volu:.5f}, 理想気体のVm:{vid:.5f}, Bを入れて計算:{Vb:.5f}')結果は以下です。
B = -3.21230e-08, 実データのVm:0.01607, 理想気体のVm:0.01647, Bを入れて計算:0.01625
B = -3.21230e-08, 実データのVm:0.00437, 理想気体のVm:0.00465, Bを入れて計算:0.00442
B = -3.21230e-08, 実データのVm:0.00155, 理想気体のVm:0.00177, Bを入れて計算:0.00150
B = -3.21230e-08, 実データのVm:0.00064, 理想気体のVm:0.00082, Bを入れて計算:0.00053
B = -3.21230e-08, 実データのVm:0.00028, 理想気体のVm:0.00044, Bを入れて計算:0.00012うまく行きました。Bのデータが共通でインプットできています。
プログラムはうまくいきましたが、想定外のことがひとつあります。
Bの値が想定よりかなり小さいということです。終了条件として係数がほぼ0なら終わるとしていましたが、どれくらい小さければ妥当か?というのが分かりません。
終了条件を「実データのVmと計算データのVmの差が実データの±10%」に変更します。
では、C以降の計算をやっていきましょう。長くなったので、整理します。
まず、Cの計算は以下でした。
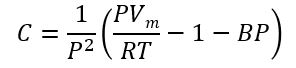
もう一つ、初めに作ったアルファベットのリストnum_ab_dicがあります。
ここでCはnum_ab_dic[2]と表せます。
Bは先ほど出したBave = -0.00009を入れます。一方で、num_ab_dic[1]はBでした。このBをBaveに置き換えることにします。つまりnum_ab_dic = {1:-0.00009, 2:C, 3:D・・25:Z}とします。
P = pres、Vm = volu、T=tempです。では、上の式は、
num_ab_dic[2] = 1/(pres^2)*(((pres * volu)/(R*temp)) – 1 – num_ab_dic[1]*pres)
となります。ではn番目ではどうなるでしょうか?
num_ab_dic[n] = 1/(pres^n)*
(((pres * volu)/(R*temp)) – 1 – num_ab_dic[1]*pres – num_ab_dic[2]*pres^2・・
– num_ab_dic[n-1]*pres^n-1)
これらを踏まえて、プログラムを書いていきます。
R = 8.314462 #気体定数[J/K・mol]
num_ab_dic = {} #数字:アルファベット辞書作成
for dic_num in range(1,26):
num_ab_dic[dic_num] = chr(ord('B')- 1 + dic_num)
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_kpa = float(data_list[1]) #圧力kPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_kpa *1000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dic
data_dic = list_input()
B_total = 0
for num, st_list in data_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
B = (1/pres) * (((pres * volu)/(R * temp))- 1) #Bの計算
B_total += B
B_ave = B_total/len(data_dic)
for num, st_list_2 in data_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
Vb = (1+ B_ave*pres)*(R*temp)/pres #Bを入れて計算
print(f'B = {B:.5f}, 実データのVm:{volu:.5f}, 理想気体のVm:{vid:.5f}, Bを入れて計算:{Vb:.5f}')
num_ab_dic[1] = B_ave
for num_ab, ab in num_ab_dic.items():
if num_ab == 1:
pass
else:
ab_total = 0
stop_count = 0 #停止のカウンター
for num, st_list_3 in data_dic.items():
temp = st_list_3[0]
pres = st_list_3[1]
volu = st_list_3[2]
kakko_nai = ((pres * volu)/(R * temp))- 1 # (pv/RT)-1
for x in range(1, num_ab):
kakko_nai -= num_ab_dic[x]*pres**x # 1~n-1まで num_ab_dic[x]*P**xを引く
ab_n = 1/(pres**num_ab)*kakko_nai
ab_total += ab_n
vid= (R*temp)/pres
ab_ave = ab_total/len(data_dic)
num_ab_dic[num_ab] = ab_ave
for num, st_list_4 in data_dic.items():
temp = st_list_4[0]
pres = st_list_4[1]
volu = st_list_4[2]
vid= (R*temp)/pres #理想気体として計算
kakko_nai_2 = 1 # V = RT/p(1+BP+・・・)の(1+)
for y in range(1, num_ab+1):
kakko_nai_2 += num_ab_dic[y]*pres**y # 1~n-1まで num_ab_dic[x]*P**xを足す
Vn = (kakko_nai_2)*(R*temp)/pres #Bを入れて計算
print(f'{ab} = {ab_ave}, 実データのVm:{volu:.5f}, 理想気体のVm:{vid:.5f}, {ab}を入れて計算:{Vn:.5f}')
if abs(Vn - volu)/volu < 0.1: #計算値ち実データの差が10%以下
stop_count +=1
if stop_count == len(data_dic): #データ数と停止カウントが同じになれば停止
break結果は以下のようになりました。
B = -3.21230e-08, 実データのVm:0.01607, 理想気体のVm:0.01647, Bを入れて計算:0.01625
B = -3.21230e-08, 実データのVm:0.00437, 理想気体のVm:0.00465, Bを入れて計算:0.00442
B = -3.21230e-08, 実データのVm:0.00155, 理想気体のVm:0.00177, Bを入れて計算:0.00150
B = -3.21230e-08, 実データのVm:0.00064, 理想気体のVm:0.00082, Bを入れて計算:0.00053
B = -3.21230e-08, 実データのVm:0.00028, 理想気体のVm:0.00044, Bを入れて計算:0.00012
C = -5.801079e-14, 実データのVm:0.01607, 理想気体のVm:0.01647, Cを入れて計算:0.01622
C = -5.801079e-14, 実データのVm:0.00437, 理想気体のVm:0.00465, Cを入れて計算:0.00425
C = -5.801079e-14, 実データのVm:0.00155, 理想気体のVm:0.00177, Cを入れて計算:0.00095
C = -5.801079e-14, 実データのVm:0.00064, 理想気体のVm:0.00082, Cを入れて計算:-0.00091
C = -5.801079e-14, 実データのVm:0.00028, 理想気体のVm:0.00044, Cを入れて計算:-0.00311
D = -2.117954e-19, 実データのVm:0.01607, 理想気体のVm:0.01647, Dを入れて計算:0.01619
D = -2.117954e-19, 実データのVm:0.00437, 理想気体のVm:0.00465, Dを入れて計算:0.00376
D = -2.117954e-19, 実データのVm:0.00155, 理想気体のVm:0.00177, Dを入れて計算:-0.00371
D = -2.117954e-19, 実データのVm:0.00064, 理想気体のVm:0.00082, Dを入れて計算:-0.02983
D = -2.117954e-19, 実データのVm:0.00028, 理想気体のVm:0.00044, Dを入れて計算:-0.13587
~~~~略~~~~
Y = -1.861479e-132, 実データのVm:0.01607, 理想気体のVm:0.01647, Yを入れて計算:0.01607
Y = -1.861479e-132, 実データのVm:0.00437, 理想気体のVm:0.00465, Yを入れて計算:-45830810.07659
Y = -1.861479e-132, 実データのVm:0.00155, 理想気体のVm:0.00177, Yを入れて計算:-2128414832921091328.00000
Y = -1.861479e-132, 実データのVm:0.00064, 理想気体のVm:0.00082, Yを入れて計算:-934630279005096276362526720.00000
Y = -1.861479e-132, 実データのVm:0.00028, 理想気体のVm:0.00044, Yを入れて計算:-14792940641579181162629375310430208.00000
Z = -7.708807e-138, 実データのVm:0.01607, 理想気体のVm:0.01647, Zを入れて計算:0.01607
Z = -7.708807e-138, 実データのVm:0.00437, 理想気体のVm:0.00465, Zを入れて計算:-150261360.90069
Z = -7.708807e-138, 実データのVm:0.00155, 理想気体のVm:0.00177, Zを入れて計算:-20431433938324135936.00000
Z = -7.708807e-138, 実データのVm:0.00064, 理想気体のVm:0.00082, Zを入れて計算:-21283973308517310443150114816.00000
Z = -7.708807e-138, 実データのVm:0.00028, 理想気体のVm:0.00044, Zを入れて計算:-690655833514079632793616296548761600.00000ぬわーーーーーーーー!
階層が下に行くほど、実データから外れていっています。どこかで間違えているのでしょうか?
いろいろプログラムをいじくって、何が起きているかわかりました。
まず、プログラムはやりたいことが出来てそうでした。
各データから算出したCの値をアウトプットしてみました。
-2.878667201893035e-13
-1.4590825661090165e-14
5.0430229979636375e-15
4.49711063850773e-15
2.8634378148513185e-15プラスとマイナスが混在しています。ここから算出されるCの平均が「-5.801079e-14」。結果的に、どのデータからも離れた値になってしまっています。
これがどんどん下に行くほど拡大していき、とてつもなくズレていってしまっています。
ちなみに近いデータ2つでやっても、Cでプラスとマイナスで分かれて、爆死します。
完全な戦略ミスです。B、C・・・は平均を取るとしたことから、次の補正項がプラスとマイナスになってしまうようです。
いやー行けると思ったのにな~。やっぱり物理的な意味を無視しちゃダメってことですかね。
まープログラムはできたのでよしとします。
また、いい方法思いついたら再チャレンジします。
(3/11追記:いい方法思い付きました!!)
Fin?
To Be Continued : 気体の状態方程式をPythonで! episode 3
PyQさんで勉強中!





コメント