
統計とグラフを駆使してプログラムを検証した!
グラフをもう少しやっていこう!!
記事①:Pythonで円周率を求めよう ~ビュフォンの針を落とす ep1~
記事②:クラスを継承して改良しよう ~ビュフォンの針を落とす ep2~
記事③:Pythonでグラフ描写して検証する ~ビュフォンの針を落とす ep3~
過去3回、「ビュフォンの針」の問題を取り上げて遊んできました。
前回は、グラフを使ってプログラムの出来を検証して、見事に?プログラム(第2回)の出来の悪さを指摘しました。
今までやってきて思うのは、「針を落としてる感」がない!!ということです。
やっていることは分かるのですが(自分でつくってるので・・)、イメージが沸かないんですよね。
そこで今回は、作成したプログラムをもとに、「針をおとす」状態をグラフで表示してビジュアルに現象を理解できるようにしたいと思います。(裏テーマPandasを使ってみよう!!)
(2021年4月24日:学習開始64日目 PyQさんで勉強中!)
前回、今回と「グラフを書く」にスポットを当ててきました。グラフ・・・
タイトル「Photograph」の曲を聴きながらやっていきたいと思います。今回は2曲。
1曲目はEd Sheeranさんのアルバム「X」より「Photograph」!
2曲目はNickelbackのアルバム「ALL THE RIGHT REASONS」より「Photograph」!
両曲ともエモーショナルな名曲ですね。やはり写真で郷愁をそそられるのは世界共通なんでしょう。
また、両方ともカラフルな印象のアルバムです。個人的に。
(曲名から公式YouTubeに飛びます。)
ベスト盤を紹介します。あえて。1曲目がPhotograph
さて、行きましょう。
1.これまでの振り返り
まずは、簡単に「ビュフォンの針」の問題を振り返りましょう。
詳細は1回目の記事にあるので省略しますが、内容は以下です。
①:間隔tで平行線が描かれている床を用意します。
②:長さl(エル)の針を床に落とします。(針は床に刺さらずに倒れるものとします。)
③:床の平行線と針が交差する確率を求めます。
で、t > lの場合、針と床の線が交差する確率は、以下のようになり円周率が現れます。

第1回では、「針先端の座標」と「角度」でシミュレーションしてうまく検証ができました。
第2回では、「角度」を使用せずに求めようとしてうまく行かず、第3回で計算の仮説が誤っていることが分かりました。
今回は、爆死した第2回のプログラムはバッサリと切って、第1回のプログラムをベースにしたいと思います。
で、今回やりたいのは、「ビュフォンの針」でやっていることをグラフ上に視覚的に表現したいと思います。
前回まで、プログラムをいろいろいじって長大になってしまいました。
一旦、ベースに戻します。第1回で作った以下のプログラムをスタートのベースにします。
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
num += 1
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
buffon_main(para.t_val, para.l_val, para.n_val)2.今回やりたい事
今回やりたいことは大きく2つです。
①:グラフに間隔tの点線を引く(=床のイメージ)
②:試行回数n本、長さlの針をグラフ上に表現する(=針を落とすイメージ)
この2つです。
あと、学習的な意味でもう一つ。「Pandas」ライブラリの使用です。
もともとやりたい事だけでいうと、Pandasは必要ない、もっというと書き方がややこしくなるだけのような気がしています。
ではなぜ使うのか?
理由は簡単。使ってみたいから、使ってみます!
3.Pandasについて 概要とインストール
「Pandas」= 「pan(el)-da(ta)-s」ということでパネル(エクセルの表のようなもの)にデータをインプットしてデータを分析するライブラリです。
データサイエンスや機械学習で必要になるそうなので、この機会に使ってみます。
「Pandas」は標準ではインストールされていません。
(Anacondaでは、はじめからインストール済みです)
では、インストールしてみましょう。
matplotlibと同様、めっちゃ簡単です!
ステップ①:コマンドプロンプトを開く。(ターミナルを開く)
ステップ②:「>」のあとに「pip install pandas」を入れて実行。
C:\Users\XXXXX>pip install pandasこれだけです!
実行して以下のように「Successfully installed pandas」が表示されれば成功です。
~~~~~略~~~~~
Installing collected packages: pytz, pandas
Successfully installed pandas-1.2.4 pytz-2021.1
(うまく出来なかった場合、どうすれば良いかは分かりません・・・悪しからず。)
4.プログラムを書いていこう①:床に線を書く
では、プログラムを書いていきましょう。
今回の「グラフを描写」というのは、ビュフォンの針のシミュレーションとはある種「独立した」プログラムになります。
こういう関係を「直交性をもつ」といい、プログラムを分離した方がメンテナンスや再利用の関係上良いそうです。(この場合はメンテナンスも再利用もあまり関係なさそうですが、、、)
グラフ描写は、メインの関数に直接入れずに別の関数として処理したいと思います。
前回使用したmatplotlibを使ってグラフを書いていきます。matplotlibは前回参照。
(前回記事:Pythonでグラフ描写して検証する ~ビュフォンの針を落とす ep3~)
今回はこのページをめっちゃ参考にさせていただきました。matplotlibのめっちゃまとめ
まずは、
「やりたい事①:グラフに間隔tの点線を引く(=床のイメージ)」
をやっていきます。
まず、床を設置します。
床に当たるグラフは一つです。複数ではなく一つのグラフに集約させたいです。
どうせならグラフ=床に色を付けましょう。色は象牙=アイボリーカラーです。
通常は、fig.subplots()としますが、色を指定したり、後々グラフ範囲を指定したりしたいので、
add_subplot()
を使用します。
from matplotlib import pyplot as plt
def graph_plot(t_val): # t:平行線の間隔
fig = plt.figure() #グラフ台紙作成
ax = fig.add_subplot(1, 1, 1, fc='ivory') #ivoruカラー指定
plt.show()
graph_plot(4)
まずはここまでを実行してみましょう。graph_plot(4)の3はt_valの仮置きです。
まだ、なにも書かれていませんが色がついています。
次は、線を引いていきましょう。
引きたい線は
・y=0、y = t、 y=2 t、 y = 3 tの3本の平行線を引きたい
・「薄い」、「赤色」の「点線」を引きたい
です。
特定の位置に平行線を引くためには、hlinesを使います。
hlinesの必要な引数は、
hlines(y = y座標、xmin = 線の左端、xmax = 線の右端)
加えて、colors:色、alpha:透明度、linestyles:線のスタイルを設定していきます。
さて、「xminとxmaxをどうするか?」という問題があります。
針の先端を落とす範囲は、x軸、y軸ともに「0~3t」と定めています。
針の末端まで考慮すると、針の存在する範囲は「ーl~3t+l」となります。
(l=針の長さ、エル)
ということは、関数の引数にl_valも設定して以下のようになりました。
from matplotlib import pyplot as plt
def graph_plot(t_val, l_val): # t:平行線の間隔
fig = plt.figure() #グラフ台紙作成
ax = fig.add_subplot(1, 1, 1, fc='ivory') #ivoruカラー指定
ax.hlines(y = [0, t_val, 2*t_val, 3*t_val],
xmin=-t_val, xmax=3*t_val+l_val ,color='red', alpha = 0.5, linestyle = '--')
# 色=赤、透明度 = 0.5、点線
plt.show()
graph_plot(4, 3)実行した結果は以下です。
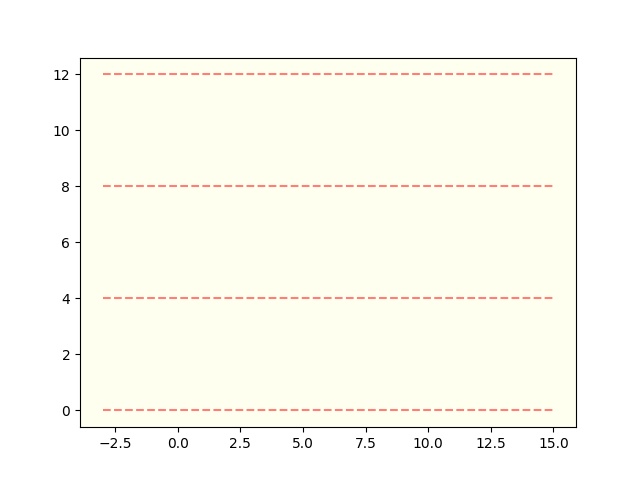
できました!!
針が落とされるところはすべて平行線が引かれたのでこれで良いのですが、両端にスキマがあるのが少し気持ち悪いですね。
これは、平行線を端まで描写するために、自動的にx軸が定まったために起こったものです。
であれば、描写エリアのx軸範囲を指定してやれば、スキマを消せそうです。
やってみましょう。add_subplotをいじります。
from matplotlib import pyplot as plt
def graph_plot(t_val, l_val): # t:平行線の間隔
fig = plt.figure() #グラフ台紙作成
ax = fig.add_subplot(1, 1, 1, fc='ivory', #ivoruカラー指定
xlim = (-l_val, 3*t_val+l_val)) #範囲指定
ax.hlines(y = [0, t_val, 2*t_val, 3*t_val],
xmin=-l_val, xmax=3*t_val+l_val ,color='red', alpha = 0.5, linestyle = '--')
# 色=赤、透明度 = 0.5、点線
plt.show()
graph_plot(4, 3)
結果は以下です。
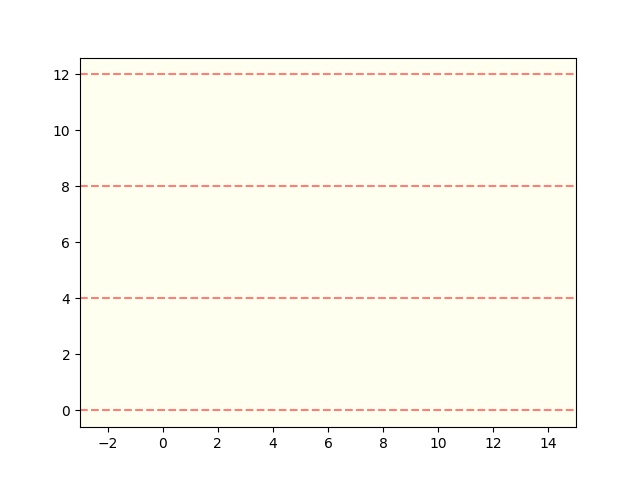
できました!!これで床線はOKですね!
5.プログラムを書いていこう②:pandasにインプット
次は、針をグラフに落としていきたいと思います。
ただし、その前に針のデータをPandasにまとめていきましょう。
一旦、グラフから離れて、元のプログラムを編集していきます。
Pandasのデータフレームに乗せるデータは、
「θ、針先端のX座標、y座標、針末端のx座標、y座標、hit判定」
(hit判定は、平行線に重なるかどうかです。)
にしたいと思います。
Hit判定をするので、分岐の中身を変えています。
メインの関数のループの中で、データフレームに1行ずつデータを加えていくようにします。
「ignore_index=True」でデータを加えるときに元のデータのインデックスを消します。
これを入れないとエラーが出ます。
データフレームをreturnで返して、dfで受ける形にします。
あと、Pandasのついでにmatplotlibもインポートしておきましょう。
import random
import math
import pandas as pd
from matplotlib import pyplot as plt
class Input_para:
~~~~~略~~~~~
def buffon_main(t_val, l_val, n_val):
df = pd.DataFrame(columns=['θ', 'x_posi', 'y_posi', 'x_end', 'y_end', 'Hit']) #データフレーム作成
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
hit_hantei = 1 #Hit判定 1ならあたり
else:
hit_hantei = 0 #Hit判定 0なら外れ
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
hit_hantei = 1
else:
hit_hantei = 0
y_2 = needle.y_change(t_val, 'ep')
df = df.append ({'θ' : needle.theta,
'x_posi' : needle.x_posi , 'y_posi' : needle.y_posi,
'x_end' : needle.endpoint(xy='x') , 'y_end' : needle.endpoint(xy='y'),
'Hit' : hit_hantei},
ignore_index=True) #ignore_index=Trueが無いとエラーになる
num += 1
~~~~~略~~~~~
print(f'円周率 : {pi}')
return df
~~~~~略~~~~~
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
df = buffon_main(para.t_val, para.l_val, para.n_val)
print(df)では、出力してみましょう!
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:10
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10
試行回数:10
交差本数:5
交差する確率 P = 2l/t(pi) = 0.5
円周率 : 3.0
θ x_posi y_posi x_end y_end Hit
0 138.508144 4.170059 1.051525 1.922910 3.039066 0.0
1 252.211500 4.024134 2.848543 3.107621 -0.008029 1.0
2 109.952277 2.684100 11.690053 1.660388 14.509984 1.0
3 155.999039 9.246508 5.222984 6.505892 6.443240 0.0
4 221.301070 6.784998 2.224131 4.531242 0.244084 0.0
5 8.128652 5.990561 3.571002 8.960421 3.995191 0.0
6 64.600007 4.891007 1.631115 6.177813 4.341121 1.0
7 127.903084 10.428442 6.299833 8.585459 8.666986 1.0
8 69.809256 6.984149 6.572613 8.019589 9.388260 1.0
9 122.479710 5.656701 0.932052 4.045698 3.462797 0.0うまくデータフレームに入力できましたね。
簡易的にグラフを出力してみましょう。
ちなみに、表示が多くなりすぎないようにdf.head()として冒頭のみ表示するようにしてます。
~~~~~略~~~~~
df = buffon_main(para.t_val, para.l_val, para.n_val)
print(df.head()) #冒頭のみ表示
df.plot()
plt.show()試行回数100でグラフを書いてみましょう。
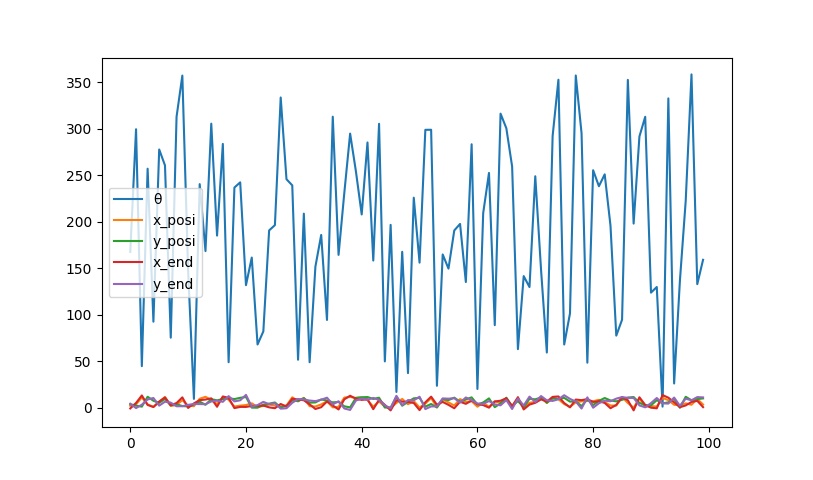
縦軸が360なので、他のデータはほぼ0に見えますね。
まあ、ここは深追いせずに、次に行きましょう。
6.プログラムを書いていこう③:針を投げよう
ついに針を投げていきます。
まずは、先ほどのメインのプログラムで針を投げます。
最終的にはグラフを統合しますが、まずはここで試します。
さて、Pandasでデータフレームを作成しましたが、普通にグラフを書くとさっき書いたグラフのように全体のデータをまとめたようなグラフになります。
ここでは、1行ずつ取り出して処理する必要があります。
1行ずつ処理するのは、pandasのitertuples()を使います。
これをforを合わせて、1行ずつ取り出せます。
ではやっていきましょう。
import random
import math
import pandas as pd
from matplotlib import pyplot as plt
~~~~~略~~~~~
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
for row in df.itertuples():
x_list = [row[2], row[4]] # row[2] = x_posi, row[4] = x_end
y_list = [row[3], row[5]] # row[3] = y_posi, row[5] = y_end
ax.plot(x_list, y_list) #始点と終点の2点間をつなぐ
plt.show()では、出力してみましょう。試行回数は20です。t=4、l=3にします。
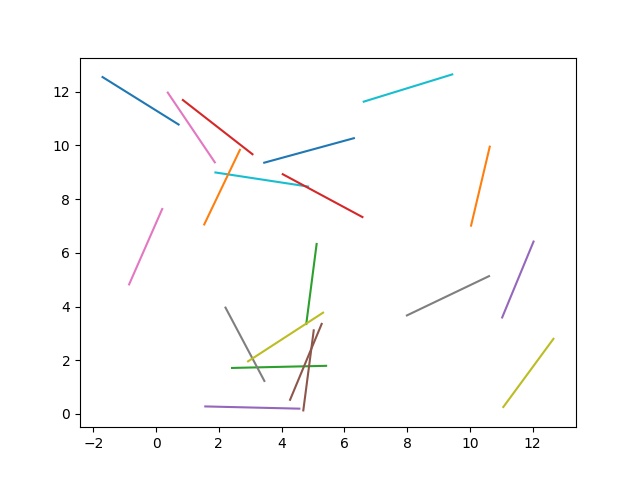
うまく出来ました。
カラフルですねぇ。これで終わっても良いくらいです。
では、統合していきましょう。
7.プログラムを書いていこう④:床に針を投げよう
統合していきましょう。
まずは、グラフ描写プログラムにまとめていきます。
graph_plot関数にまとめますが、引数としてdfを入れます。
(引数としてデータフレームを入れれるか不安でしたが、大丈夫でした!)
def graph_plot(t_val, l_val, df): # t:平行線の間隔, df:針のデータ
fig = plt.figure() #グラフ台紙作成
ax = fig.add_subplot(1, 1, 1, fc='ivory', #ivoruカラー指定
xlim = (-l_val, 3*t_val+l_val)) #範囲指定
ax.hlines(y = [0, t_val, 2*t_val, 3*t_val],
xmin=-l_val, xmax=3*t_val+l_val ,color='red', alpha = 0.5, linestyle = '--')
# 色=赤、透明度 = 0.5、点線
for row in df.itertuples():
x_list = [row[2], row[4]] # row[2] = x_posi, row[4] = x_end
y_list = [row[3], row[5]] # row[3] = y_posi, row[5] = y_end
ax.plot(x_list, y_list) #始点と終点の2点間をつなぐ
plt.show()次にこれをメインに統合します。
import random
import math
import pandas as pd
from matplotlib import pyplot as plt
class Input_para:
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
def graph_plot(t_val, l_val, df): # t:平行線の間隔, df:針のデータ
~~~~~略~~~~~
def buffon_main(t_val, l_val, n_val):
~~~~~略~~~~~
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
df = buffon_main(para.t_val, para.l_val, para.n_val)
print(df.head()) #冒頭のみ表示
graph_plot(para.t_val, para.l_val, df)これで実行していきます。試行回数は20にします。
出力されるグラフはこうなります。
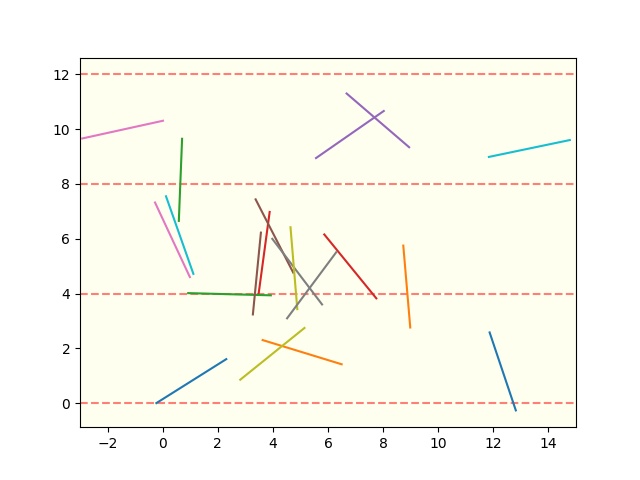
ほぼ出来ましたね。あともう少し。
平行線に当たった針と外れた針の色を分けたいと思います。
ここで、データフレームで設定した「Hit」を使います。
当たりは金色、外れは銀色としましょう。
次で完成です。全プログラムは以下です。
import random
import math
import pandas as pd
from matplotlib import pyplot as plt
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
def graph_plot(t_val, l_val, df): # t:平行線の間隔, df:針のデータ
fig = plt.figure() #グラフ台紙作成
ax = fig.add_subplot(1, 1, 1, fc='ivory', #ivoruカラー指定
xlim = (-l_val, 3*t_val+l_val)) #範囲指定
ax.hlines(y = [0, t_val, 2*t_val, 3*t_val],
xmin=-l_val, xmax=3*t_val+l_val ,color='red', alpha = 0.5, linestyle = '--')
# 色=赤、透明度 = 0.5、点線
for row in df.itertuples():
x_list = [row[2], row[4]] # row[2] = x_posi, row[4] = x_end
y_list = [row[3], row[5]] # row[3] = y_posi, row[5] = y_end
if row[6] == 1:
ax.plot(x_list, y_list, c = 'gold') #始点と終点の2点間をつなぐ
else:
ax.plot(x_list, y_list, c = 'silver') #始点と終点の2点間をつなぐ
plt.show()
def buffon_main(t_val, l_val, n_val):
df = pd.DataFrame(columns=['θ', 'x_posi', 'y_posi', 'x_end', 'y_end', 'Hit']) #データフレーム作成
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
hit_hantei = 1 #Hit判定 1ならあたり
else:
hit_hantei = 0 #Hit判定 0なら外れ
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
hit_hantei = 1
else:
hit_hantei = 0
y_2 = needle.y_change(t_val, 'ep')
df = df.append ({'θ' : needle.theta,
'x_posi' : needle.x_posi , 'y_posi' : needle.y_posi,
'x_end' : needle.endpoint(xy='x') , 'y_end' : needle.endpoint(xy='y'),
'Hit' : hit_hantei},
ignore_index=True) #ignore_index=Trueが無いとエラーになる
num += 1
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
return df
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
df = buffon_main(para.t_val, para.l_val, para.n_val)
print(df.head()) #冒頭のみ表示
graph_plot(para.t_val, para.l_val, df)試行回数はまず5にします。
まずは出力されるデータです。
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:5
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 5
試行回数:5
交差本数:2
交差する確率 P = 2l/t(pi) = 0.4
円周率 : 3.75
θ x_posi y_posi x_end y_end Hit
0 162.826030 2.107571 8.391832 -0.758667 9.277654 0.0
1 236.062049 10.818082 7.998004 9.143198 5.509076 0.0
2 183.349934 11.754422 4.169638 8.759549 3.994336 1.0
3 149.239111 5.264485 10.031754 2.686557 11.566123 0.0
4 257.392000 11.472965 2.814701 10.818127 -0.112958 1.0次にグラフです。Hitは2ですね。
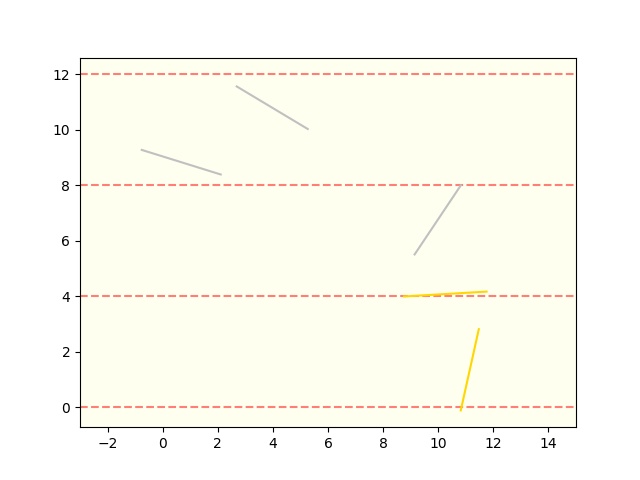
グラフは平行線に乗った2つの針が金色になっています。
1つはギリギリですね。値をみると7.998004、確かにギリギリ。
試行回数を増やしていくつかグラフを出力してみましょう。
試行回数=20
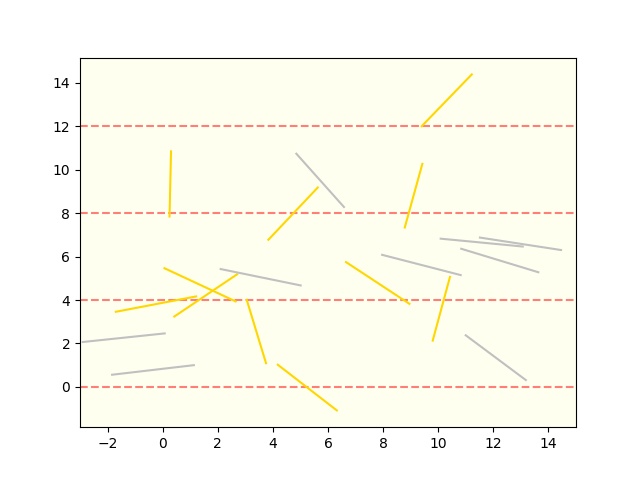
試行回数=100。それっぽくなりました。
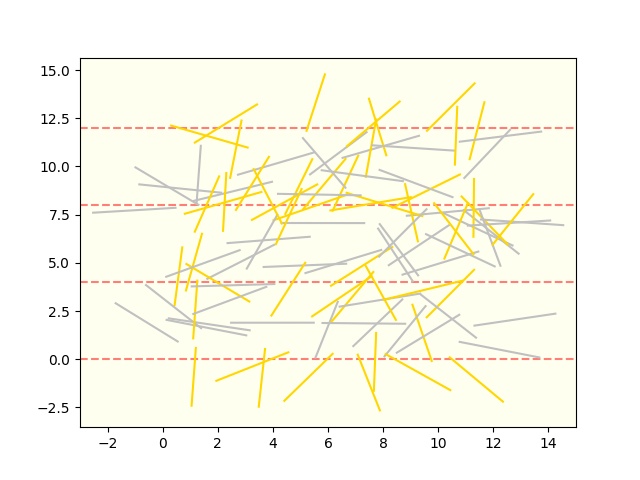
試行回数=1000。ハリネズミみたいになりましたね。いや文字通りハリセンボンか。
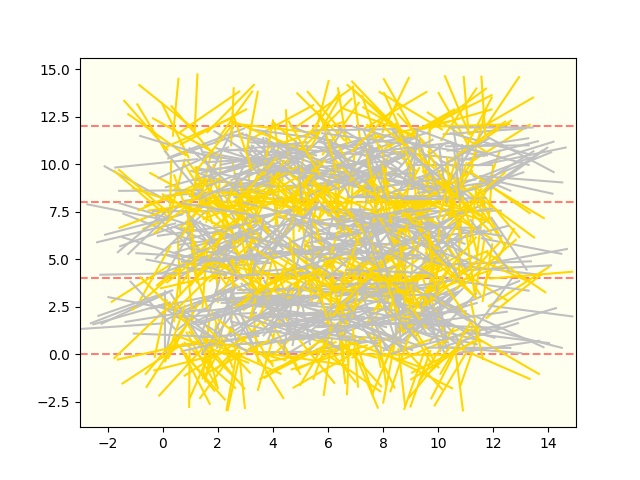
試行回数=10000。たわしです。
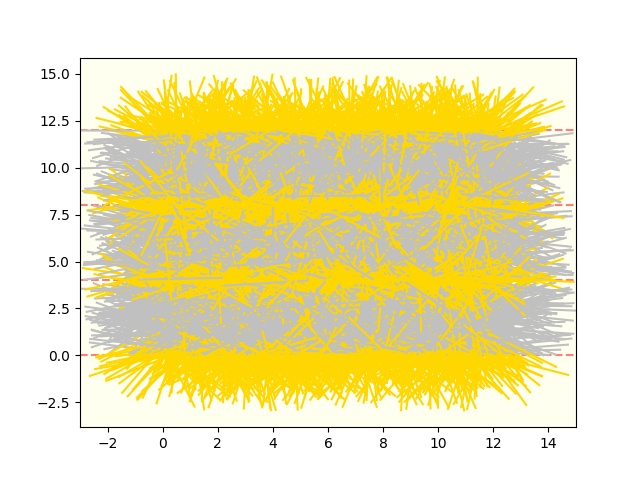
試行回数=100000。なんじゃこりゃー。さすがにキモイなあ。
というか、ここまでやると出力するのに時間がかかってしまいました。
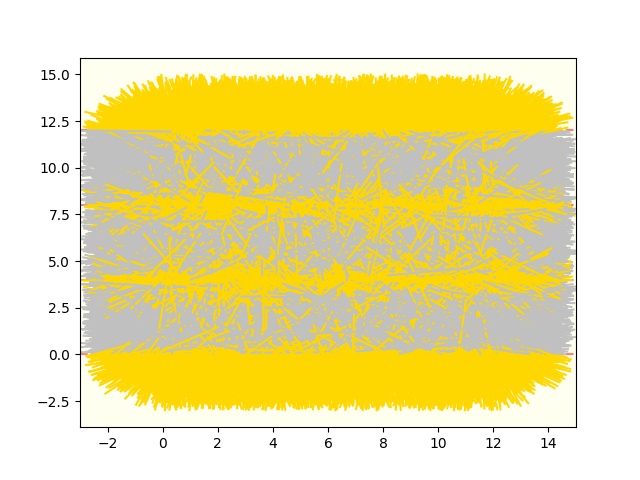
こうやって視覚的にみると、状態が良く分かりますね。
【教訓】針を投げすぎてはいけない。
「ビュフォンの針」でやりたいことは大体やりましたね。これにて終了!
FIN.
PyQさんで勉強中!




コメント