
シミュレーションの古典的問題「ビュフォンの針」
古典はやっとかないとね!!
「ビュフォンの針」という問題をご存じでしょうか?
私もプログラミングのネタ探しの中で見つけた、数学の問題です。
この問題の面白いところは、「円周率」を計算で求められるところです!!
そして、もう一つ、この問題はシミュレーションにより近似的に解ける問題としても有名です。
もうやってみるしかないですよね!!(裏テーマ、グラフを書いてみよう!もあります。)
(2021年4月9日:学習開始49日目、PyQさんで勉強中!)
今回は針にまつわる曲を聴きながら行きましょう。
顔を隠して圧倒的な歌唱力で歌う現代の歌姫Siaさんのアルバム「1000 Forms of Fear」から、「Eye of the Needle」です。(曲名から公式YouTubeに飛びます。)
では行きましょう!!
1.ビュフォンの針とは?
まず、「ビュフォンの針」とはどのような問題かをみていきましょう。
問題の内容は以下です。参照:Wikipedia ビュフォンの針
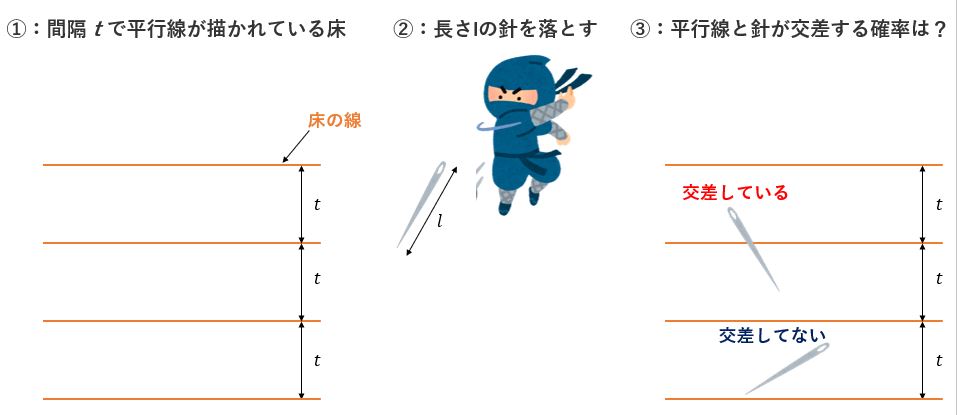
①:間隔tで平行線が描かれている床を用意します。
②:長さl(エル)の針を床に落とします。(針は床に刺さらずに倒れるものとします。)
③:床の平行線と針が交差する確率を求めます。
絵で表現するとこんな感じです。忍者に針を投げてもらいました。
この問題の数学的解法は、Wikipediaにもありますし、多数解説があるのでそちらに譲るとして、
結論だけ書くと、

となります!!
(あ、t ≧ l の場合です。t< l の場合もWikipediaにありますが、ややこしいのでパス)
なんと、円周率が現れてました!!
今回は、これをシミュレーションして求めてみたいと思います。
ちなみに、乱数(ランダム)を用いてシミュレーションしていきますが、この手法は「モンテカルロ法」というそうです。
モンテカルロ=モナコ公国の地区名で、カジノで有名なところです。
ランダム → カジノ → モンテカルロ ってどうなんでしょう。個人的には嫌いじゃないです。
2.作戦会議 どうやって説く?
問題の内容は分かりました。次は解法を考えていきましょう。
まずは、ルールの内容をそのまま理解してみましょう。
はじめに「間隔tの平行線が書かれている床」があります。ふむふむ。そのままです。
つぎに、「床に針を落とします」。さて、「床のどこに?」落とすのでしょうか?
床にxとyの座標があるとすると、どこかの平行線の間に存在する、とある1点(x、y)に針先が落ちたとします。ただし、平行線に平行方向をx、垂直方向をyとします。
その後、「針はランダムな方向に倒れる」としましょう。ここでは、平行線に対して角度θとなるように倒れたとします。
ここまでを図で書いてみるとこんな感じです。
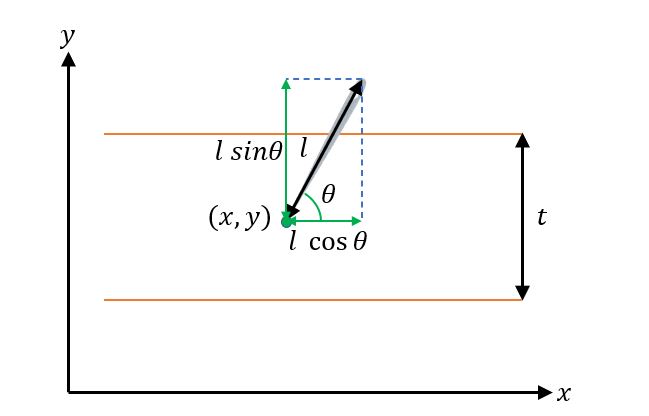
少しずつ見えてきましたね。lsinθ が重要そうですね。
もう少し、条件設定してみましょう。以下の条件で考えてみます。
条件①:4本の平行線(Line①~Line④)を考えて、針はその中に落とされるとする。
条件②:Line①は原点(0, 0)を通る。
条件③:針は(3t, 3t)の正方形の領域内に落とされるとする。
特に、平行線の数を4本にした意味はありません。
結局、どこに落とされたとしても、2本の平行線と落とされたポイント、θの角度だけで決まるので、最小2本の線を考慮すれば解決できます。
まあ、今回は4本でやってみます。ここまでを図示してみましょう。
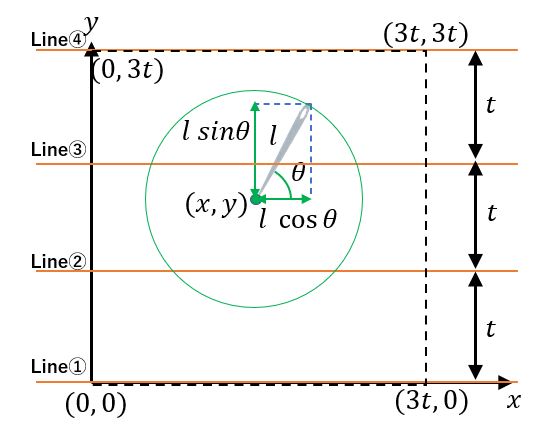
かなり条件が明確になってきました。
では、針と平行線が交差する条件を考えていきましょう。
まずは図示して考えてみましょう。交差する境界条件を考えてみます。
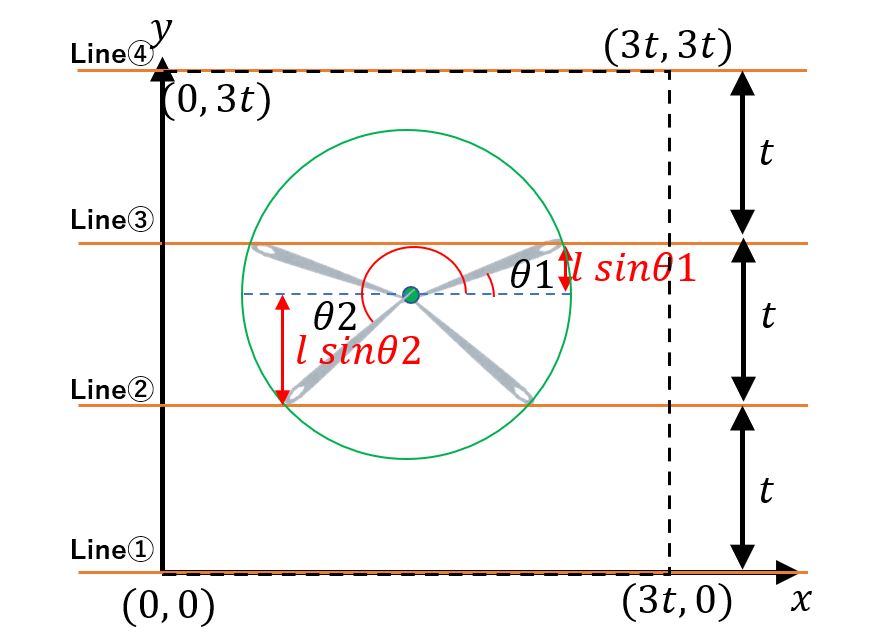
この図では、t<y<2tの場合になります。
この図で分かるのは、「0° ≦ θ< 180°の場合」と「180° ≦ θ< 360°の場合」で分けると良さそうです。
場合分けして考えてみましょう。
(1)0° ≦ θ< 180°の場合(図ではθ1)
θが180°以下の場合、針の先端は(x, y)とすると、末端は(x + lcosθ1, y + lsinθ1)となります。
この場合は、Line③と交差するかどうかを考えれば良さそうです。
・y + lsinθ1 ≧ 2t ならば交差する
・y + lsinθ1 < 2t ならば交差しない
(2)180° ≦ θ< 360°の場合(図ではθ2)
θが180°より大きい場合、sinθ2はマイナスの値を取ります。
針の先端は(x, y)とすると、末端は(x + lcosθ2, y + lsinθ2)となります。θの値に関わらず同じですね!
この場合は、Line②と交差するかどうかを考えれば良さそうです。
・y + lsinθ1 ≦ t ならば交差する
・y + lsinθ1 > t ならば交差しない
ポイントは(1)の場合と大小の向きが逆になっている点をですね。
あとは、最初に針が落ちる位置でyの値が「0~t」、「t~2t」、「2t~3t」で分ければ良さそうです。
ちなみに、Wikipediaにも記載がありますが、円周率πを求めるのにsinθを使用するのは問題があります。この点は後で考えるとして、ここまでに検証した内容でやってみましょう!!
3.フローチャートを書いてみよう
ここまでに考えた事をそのままフローチャートにまとめてみました。
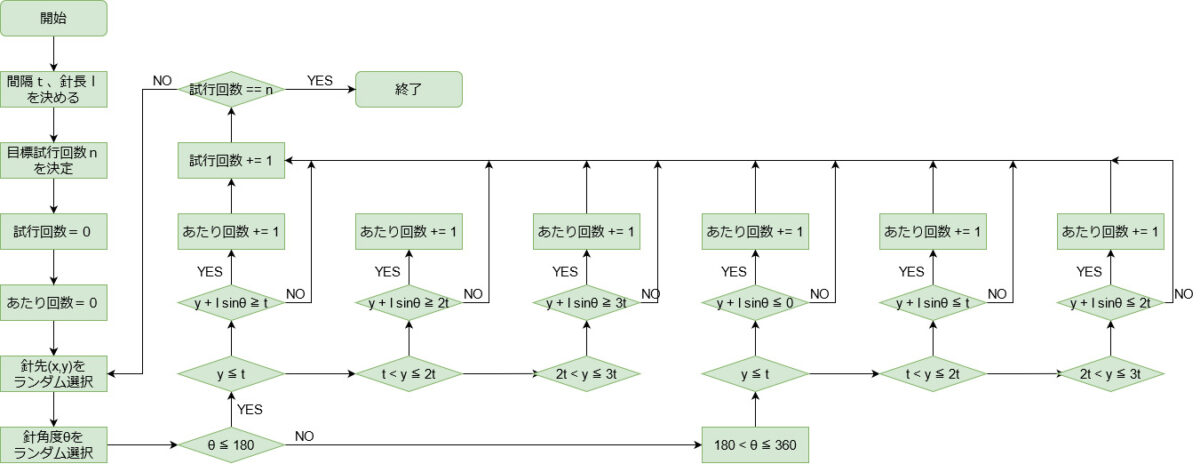
見づらいですねぇ。
やっていることは、単純ですが、分岐が多いですね。このまま進めてもよいのですが、もう少し工夫をしましょう。
θ ≦ 180°の場合で考えてみます。交差する条件は、
①:0 < y ≦ t → y + lsinθ1 ≦ t
②:t < y ≦ 2t → y + lsinθ1 ≦ 2t
③:2t < y ≦ 3t → y + lsinθ1 ≦ 3t
①はそのまま、②は両辺からtを引く、③は両辺から2tを引くとすれば、すべて①の式にまとめれそうです。
yの値が0 ≦ y ≦ tに収まるようにします。
そうすると角度の分岐以降の計算がひとつにまとまります。
フローチャート改はこのようになりました。
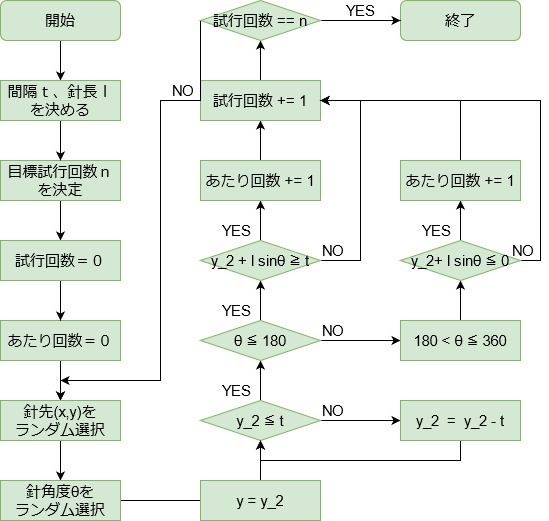
大幅に簡素化されましたね。これで行きましょう。
4.プログラムを書いていこう
では、プログラムを書いていきましょう。
今回、三角関数の計算を行います。三角関数の計算は「mathモジュール」で行います。
また、針位置の決定には「randomモジュール」も使用します。
まずは、「間隔t、針の長さl、目標試行回数nの決定」です。
さらに、「試行回数=0」、「あたり回数=0」までやってしまいましょう。
import random
import math
def t_input():
while True:
t_str = input('間隔 t =') #tの入力
try:
t_flo = float(t_str) #floatで設定
return t_flo #floatで返す
break
except ValueError:
print('数字を入力してください')
def l_input():
while True:
l_str = input('針の長さ l =') #lの入力
try:
l_flo = float(l_str) #floatで設定
return l_flo #floatで返す
break
except ValueError:
print('数字を入力してください')
def n_input():
while True:
n_str = input('試行回数 N =') #nの入力
try:
n_int = int(n_str) #intで設定
return n_int #intで返す
break
except ValueError:
print('数字を入力してください')
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定入力は、それぞれ関数定義しています。
ここで、入力値は文字列になっているので、tとlは小数に、試行回数nは整数に変換しています。
気になるのは、同じことを繰り返し書いてしまっていることです。
classでまとめれるはずです。やってみましょう!
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定できました。半分くらいで納める事が出来ています。
やはり「オブジェクト指向」は偉大です。
※ちなみに、「オブジェクト指向」は「オブジェクト指向でなぜ作るのか」で学習しました。
どこで使えばよいのかが明確になる名著だと思います。
【書籍紹介】オブジェクト指向でなぜつくるのか
さて、次に行きましょう。
次は針を落とす段階です。「針先(x、y)をランダムで決定」と「針角度θをランダムで決定」です。「針の位置」にまつわるものは、class 「Needle」でまとめましょう。
なお、「針の末端位置」もここで計算してしまいます。
~~~~~略~~~~~
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
~~~~~略~~~~~
一度、ここまでのプログラムを動かしてみましょう。ここまでを合算して下のプログラムをつけ足して実行します。
なお、正しさを検証するために、xとyの位置から針の長さを逆算したものをつけています。
~~~~~略~~~~~
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
limit = 3*para.t_val #xとyの最大値は 3t
needle = Needle(n_len = para.l_val, x_lim = limit, y_lim = limit)
print(f'初期x {needle.x_posi}')
print(f'初期y {needle.y_posi}')
print(f'初期θ {needle.theta}')
needle.throw() #針を投げて、x、y、θを再設定
print(f'投げ後x {needle.x_posi}')
print(f'投げ後y {needle.y_posi}')
print(f'投げ後θ {needle.theta}')
print(needle.endpoint('x'))
print(needle.endpoint('y'))
#三平方の定理から針の長さを計算 math.sqrt()で平方根を計算
hd_len_2jyou = (needle.x_posi - needle.endpoint('x'))**2 + (needle.y_posi - needle.endpoint('y'))**2
print(f'計算針長 {math.sqrt(hd_len_2jyou)}')実行結果は以下です。
間隔 t を入力:5
針の長さ l を入力:3
試行回数 n を入力:10
間隔 t :5.0, 針の長さ l : 3.0, 試行回数 n : 10
初期x 0
初期y 0
初期θ 0
投げ後x 14.508026543476056
投げ後y 10.053292893428596
投げ後θ 71.91566627354652
15.439276104534393
12.905094824669378
計算針長 3.0うまく行けています。今の出力用のprintは削除して、先に進みましょう。
次は、「y_2の設定」です。
さらに、「0 < y_2 < tになるように、yから間隔tを複数回引いてy_2を設定する」作業です。
これも、Needleクラスの中でやってしまいましょう。
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
~~~~~略~~~~~これで、y_2の値とその場合の末端の点が出せました。
ここまで来ると下準備は終わりです。メインの関数に進みましょう。
「θが180°以下かどうか?」で分岐させます。
次に「tとの比較」もしくは「0との比較」で交差の判定です。
「交差のカウント」と「試行回数カウント」の増加、「目標試行回数になるまでのループ」を行います。
いっきに行ってしまいましょう。
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
num += 1 #
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')これでほぼ完成です。
今までのプログラムをすべて合算します。
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
num += 1 #
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
buffon_main(para.t_val, para.l_val, para.n_val)では、実行してみましょう。
一旦、t=4、l=3としてnを変えていってみましょう。
(tとlの値に大きな意味はないですが、t>lにしないと確率がややこしくなります。)
n =10、円周率2.5、まだまだ遠いですね。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10
試行回数:10
交差本数:6
交差する確率 P = 2l/t(pi) = 0.6
円周率 : 2.5n = 100、円周率3.65、まだ遠いですね。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 100
試行回数:100
交差本数:41
交差する確率 P = 2l/t(pi) = 0.41
円周率 : 3.658536585365854n = 1000、円周率3.09、ちょっと近づいたかな。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 1000
試行回数:1000
交差本数:485
交差する確率 P = 2l/t(pi) = 0.485
円周率 : 3.0927835051546393n = 10000、円周率3.14136、かなり近づいてきました。ここまでくれば十分でしょう。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000
試行回数:10000
交差本数:4775
交差する確率 P = 2l/t(pi) = 0.4775
円周率 : 3.141361256544503n = 100000、円周率3.14432、あれ?遠のいた?
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 100000
試行回数:100000
交差本数:47705
交差する確率 P = 2l/t(pi) = 0.47705
円周率 : 3.144324494287811n = 1000000、円周率3.14543、あれ?もっと遠のいた?
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 1000000
試行回数:1000000
交差本数:476882
交差する確率 P = 2l/t(pi) = 0.476882
円周率 : 3.145432203354289n = 10000000、円周率3.14190、近づきましたね。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000000
試行回数:10000000
交差本数:4774171
交差する確率 P = 2l/t(pi) = 0.4774171
円周率 : 3.141906731032466これくらいでしょうか。
円周率3.14までは試行回数10000回で出ますが、それより小さい桁になると試行回数を増やしてもブレるようです。
確かに針を落とすシミュレーションから、円周率が求まりました。
しかし、途中でスルーしましたが「円周率を求めるのにsin、cosを使っている」という問題があります。
次回は、まずここから解消していきましょう。
To Be Continued : ビュフォンの針を落とす ep2
PyQさんで勉強中!





コメント