
前回、プログラムを改変したら円周率が求まらなくなった。
なぜダメだったのかを検証していこう!!
記事①:Pythonで円周率を求めよう ~ビュフォンの針を落とす ep1~
記事②:クラスを継承して改良しよう ~ビュフォンの針を落とす ep2~
第1回で「ビュフォンの針」をシミュレーションしたら、円周率が求められました。
しか~し、第2回で、θを使わずに計算しようとして、円周率が求まらなくなりました。
プログラム自体はきっちり動いています。
今回、なぜダメになったのかを検証していきます。
これが、データサイエンスだ!!(違うか。)
(2021年4月17日:学習開始57日目 PyQさんで勉強中!)
いままで、たくさんの針を堕としてきましたね!もう針は堕としたくない!
Dannie Mayの「針よ墜とせぬ、暮夜の息」を聞きながら検証していきましょう。
まだ、デビューして2年もたってない、超おしゃれなバンド?グループ?
いや、「Dannie May」!
(曲名から公式YouTubeに飛びます。いまから注目しておくとおそらく自慢できます!)
では検証スタート!!
1.前回の振り返り
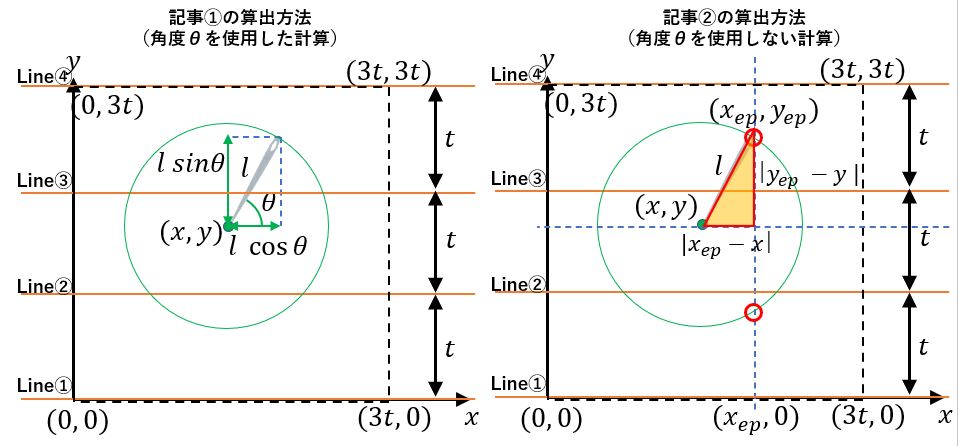
まずは、簡単に「ビュフォンの針」の問題を振り返りましょう。
詳細は1回目の記事にあるので省略しますが、内容は以下です。
①:間隔tで平行線が描かれている床を用意します。
②:長さl(エル)の針を床に落とします。(針は床に刺さらずに倒れるものとします。)
③:床の平行線と針が交差する確率を求めます。
で、t > lの場合、針と床の線が交差する確率は、以下のようになり円周率が現れます。

過去2回で異なった算出方法で計算していきました。
ポイントは、「角度θを使用するか?、しないか?」です。
結果、θを使用する手法では正しい円周率が求まり、θを使用しない手法では正しい円周率が求まりませんでした。
今回は、この理由を検証します!!
2.検証方法を考える
過去2回で、2つのプログラム(統合しているので実際は1つ)を作成しました。
違いは、針に関するclassが主体で、その他はほぼ変更していません。
では、違いを比べてみましょう。
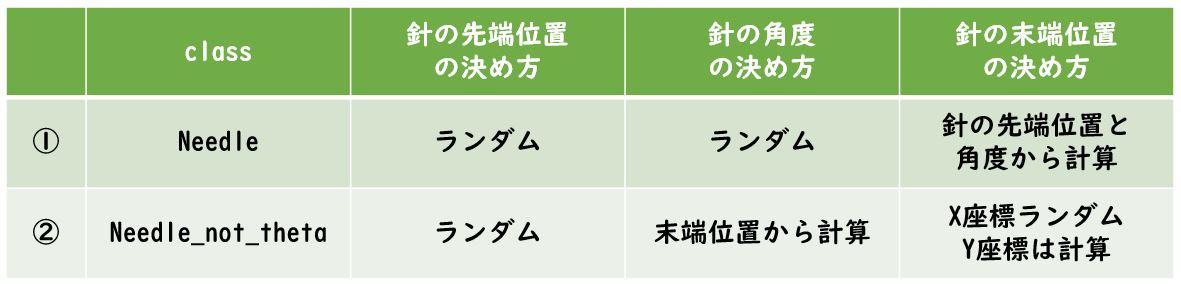
ポイントは、「角度」と「針の末端位置」の算出方法にありそうです。
この辺りを検証していきましょう!
検証の手法は、
①:統計的手法による検証 (平均、中央値、標準偏差の算出)
②:グラフ表示による検証 (分布のビジュアル化)
という2つの手法を試してみたいと思います。
では、やっていきましょう。
3.前回プログラム
まず、前回のプログラムを振りかえってみましょう。
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0 , x_ep = 1, y_ep = 0):
super().__init__(n_len, x_lim, y_lim, x_posi, y_posi, theta) #x_ep、y_ep以外は親クラスのまま super()で呼び出し
self.x_ep = x_ep #x末端座標定義
self.y_ep = y_ep #y末端座標定義
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
cos_theta = x_ep_len/self.n_len # cosθ = x座標距離 / 針長さl
theta_dg = math.degrees(math.acos(cos_theta)) #cosθ > θ(ラジアン) > θ(degree)
self.theta = y_ep_pm * theta_dg # 180°以上ならy_ep_pmは-1
if self.theta < 0:
self.theta +=360 #180°以上なら、-theta+360
def endpoint(self, xy = 'y'):
x_ep = self.x_ep #x_epはthrowで計算済み
y_ep = self.y_ep #y_epはthrowで計算済み
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle_not_theta(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
num += 1 #
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
buffon_main(para.t_val, para.l_val, para.n_val)
102行目で「どちらのクラスを選択するか?」=「どのようにして針の位置を決めるか?」を選択しています。上に表示されているのは、「Needle_not_theta」つまりθを使わず算出したものになります。
以降、ややこしいので、
クラス① :class「Needle」、θを使った算出方法
クラス② :class「Needle_not_theta」、θを使わない算出方法
とします。
これまで同様、「針の長さl = 4」、「間隔t=3」とします。
また、試行回数は過去の結果から、クラス①では10000回程度である程度正しい園主率が算出できていたので、「試行回数n =10000」とします。
4.検証①:統計的手法による検証
検証を進めていきましょう!
まずは、統計的手法です。
調べてみると、統計計算が出来るライブラリとして「statistics」と「numpy」が挙がっています。
今回は、「statistics」でやってみましょう。(numpyは今後固めて使いそうなので。)
検証したいのは、「x」「y」「θ」の値です。
このうち、「θ」はこのままデータを取得して計算していきます。
「x」と「y」については、工夫が必要です。
針の先端「x_ep」と「y_posi」がランダムに選択されているので、針末端「x_ep」と「y_ep」は計算手法が異なったとしても、先端位置に依存してランダムな値をとると予想されます。
そのため、「座標間距離」= 「末端座標ー先端座標の絶対値」で検証したいと思います。
具体的には、
・検証するx値 = 「x_len」= |「x_ep」ー「x_ep」|
・検証するy値 = 「y_len」= |「y_ep」ー「y_ep」|
とします。
元プログラムでは、while構文で目標試行回数までループをしています。
1ループごとに、「x」「y」「θ」の値をリストで取り出していきます。
では、プログラムに起こしていきましょう。
難しくないので、一気に行きます。
import statistics
import random
import math
class Input_para:
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
~~~~~略~~~~~
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
theta_list = [] #角度θのリスト
len_x_list = [] #x座標間距離のリスト
len_y_list = [] #y座標間距離のリスト
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
theta_list.append(needle.theta) #角度θのリスト出力
len_x = abs(needle.x_posi - needle.endpoint(xy='x')) #x座標間距離計算
len_y = abs(needle.y_posi - needle.endpoint(xy='y')) #x座標間距離計算
len_x_list.append(len_x) #x座標間距離のリスト出力
len_y_list.append(len_y) #y座標間距離のリスト出力
num += 1
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
~~~~~略~~~~~
for v, i in ['θ', 'x_len', 'y_len'], [theta_list, len_x_list, len_y_list]:
ave = statistics.mean(i) #平均値
med = statistics.median(i) #中央値
std = statistics.stdev(i) #標準偏差
print(f'{v} : 平均{ave:.3f}, 中央値{med:.3f}, 標準偏差{std:.3f}')
では実行してみましょう。エラーが出ました。
for v, i in ['θ', 'x_len', 'y_len'], [theta_list, len_x_list, len_y_list]:
ValueError: too many values to unpack (expected 2)forの書き方が正しくないようです。
こういう場合、「zip関数」を使う必要があるようです。
では、修正版です。
~~~~~略~~~~~
v_list = ['θ', 'x_len', 'y_len']
v_output_list = [theta_list, len_x_list, len_y_list]
for (v, i) in zip(v_list, v_output_list):
ave = statistics.mean(i) #平均値
med = statistics.median(i) #中央値
std = statistics.stdev(i) #標準偏差
print(f'{v} : 平均{ave:.3f}, 中央値{med:.3f}, 標準偏差{std:.3f}')
では実行していきましょう。クラス①の場合です。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000
試行回数:10000
交差本数:4758
交差する確率 P = 2l/t(pi) = 0.4758
円周率 : 3.1525851197982346
θ : 平均179.674, 中央値179.810, 標準偏差103.881
x_len : 平均1.912, 中央値2.114, 標準偏差0.925
y_len : 平均1.904, 中央値2.129, 標準偏差0.930
やはり、円周率3.15と近い値が求まっています。
「θ」は平均、中央値ともに約180、標準偏差103となりました。
標準偏差が大きい値ですが、ランダムに選んでいるので、ばらついていて当然です。
「x」と「y」はともに、平均1.9、中央値2.1、標準偏差0.9となりました。
ここから読み取れるのは、
・「x」「y」の平均、中央値、標準偏差がほぼ同じ =「x」と「y」は等価
・「x」「y」の平均、中央値は針長さ3の半分の1.5ではない。
ということです。
では、「x」「y」の平均、中央値はなにを表すのでしょうか?
これは、l sin45° = l cos 45° = 3 X 0.7 = 2.1であると考えられます。
では、続いて、クラス②の場合です。
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000
試行回数:10000
交差本数:5857
交差する確率 P = 2l/t(pi) = 0.5857
円周率 : 2.5610380740993683
θ : 平均180.423, 中央値184.876, 標準偏差97.688
x_len : 平均1.485, 中央値1.477, 標準偏差0.866
y_len : 平均2.367, 中央値2.611, 標準偏差0.666
あらためて、円周率2.56という誤った値が出ています。
「θ」は平均180、中央値185、標準偏差98となりました。
クラス①の結果と少し差がありますが、顕著な差には見えません。
「x」は平均1.5、中央値1.5、標準偏差0.9となりました。
「y」は平均2.4、中央値2.6、標準偏差0.7となりました。
ここから読み取れるのは、
・「x」「y」の平均、中央値、標準偏差が異なる =「x」と「y」は等価ではない
・「x」の平均、中央値は針長さ3の半分の1.5になっている。
ここにきて、クラス①と差が出てきました。
針のx末端座標を針の長さからランダムで決めたので、「x」の平均は針の長さの半分の値となっております。
「x」の平均<「y」の平均ということは、針は垂直に向きやすくなってしまっています。
つまり、床の横線と交差しやすい状態になってしまっています。
結果、交差する確率が上昇し、求まる円周率の値が誤ったものになったと考えられます。
だんだん、問題の様相が分かってきました。
つづいて、グラフで見ていきたいと思います。
5.検証②:グラフ表示による検証
グラフ表示をおこなった、目に見える形にして検証していきます。
pythonでグラフ表示をするには、「matplotlib」ライブラリを使用します。
matplotlibライブラリは、標準では入っていないライブラリなので、インストールが必要です。
windowsであれば、「コマンドプロンプト」を開いて以下を入れれば、インストールできます。
めっちゃ簡単ですね!!
C:\Users\XXXXXXX>pip install matplotlib
ここまでが下準備です。
では、先ほど作成したプログラムをもとにグラフを書いていきます。
すでに、「x」「y」「θ」のリストは作成済みなので、これをグラフ表示すれば良いですね。
さて、matplotlibは多様なグラフを描写することが出来ます。
折れ線グラフ、棒グラフ、散布図などが書けますが、今回は、「ヒストグラム」が適切です。
ヒストグラムとは、「ある区間ごとの数値の個数を積み上げたグラフ」です。
データのばらつきを見るのに適しています。
説明より実際にグラフをみた方が分かりやすいので早速プログラムに書いていきましょう。
今回もプログラム自体は簡単なので、いっきに行きます。
まずは、θのグラフを描写します。
from matplotlib import pyplot as plt
import statistics
import random
import math
class Input_para:
class Input_para:
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
~~~~~略~~~~~
theta_list = [] #角度θのリスト
len_x_list = [] #x座標間距離のリスト
len_y_list = [] #y座標間距離のリスト
def buffon_main(t_val, l_val, n_val):
~~~~~略~~~~~
print(f'{v} : 平均{ave:.3f}, 中央値{med:.3f}, 標準偏差{std:.3f}')
plt.hist(theta_list, bins=360) #θのヒストグラム 1°ごとに分割
plt.xlabel('θ') #x軸ラベル θ
plt.ylabel('freq') #y軸ラベル freq
plt.show() #グラフ描写
変えたのは、5行のみ、うち1つは冒頭のimportなので実質4行ですね。
bin = 360とすることで、値を360分割=1度ごとに分割しています。
それ以外は、グラフのx軸とy軸のラベルです。
では、出力してみましょう。
まずは、クラス①の場合です。
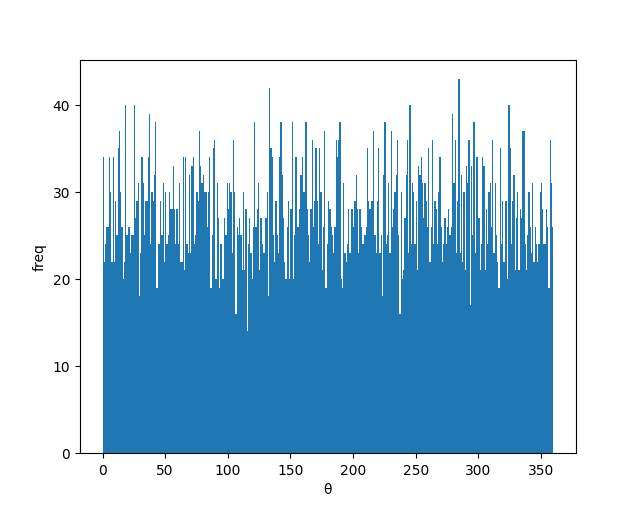
よっしゃーー、グラフ書けた!!
うまくできています。では、次にクラス②の場合です。
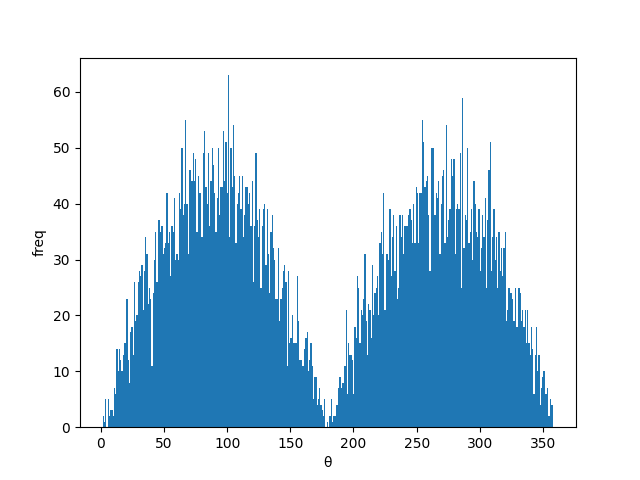
違いは一目瞭然ですね。
クラス①では、θが0~360°の間でほぼ均一に存在しています。
一方で、クラス②では、0°、180°、360°の値が極端に少なく、90°と270°付近で極大になっています。
このグラフだと、180°付近は少ないのですが、平均値、中央値は180°となってしまいますね。
続いて、「x」と「y」も同様に表示していきたいと思います。
次は、横並びで2つのグラフを描写するプログラムを書いていきます。
~~~~~略~~~~~
print(f'{v} : 平均{ave:.3f}, 中央値{med:.3f}, 標準偏差{std:.3f}')
fig = plt.figure() #描写エリア設定
ax= fig.subplots(1, 2) #横並びに2つのグラフ設定
ax[0].hist(len_x_list, bins = 50) #グラフ1にxのグラフ、50分割
ax[0].set_xlabel('x_len') #グラフ1のx軸ラベル変更
ax[0].set_ylabel('freq') #グラフ1のy軸ラベル変更
ax[1].hist(len_y_list, bins = 50) #グラフ2にxのグラフ、50分割
ax[1].set_xlabel('y_len') #グラフ2のx軸ラベル変更
plt.show() #グラフ描写
グラフを横並びにするのに少し工夫をしています。では、グラフを描写していきましょう。
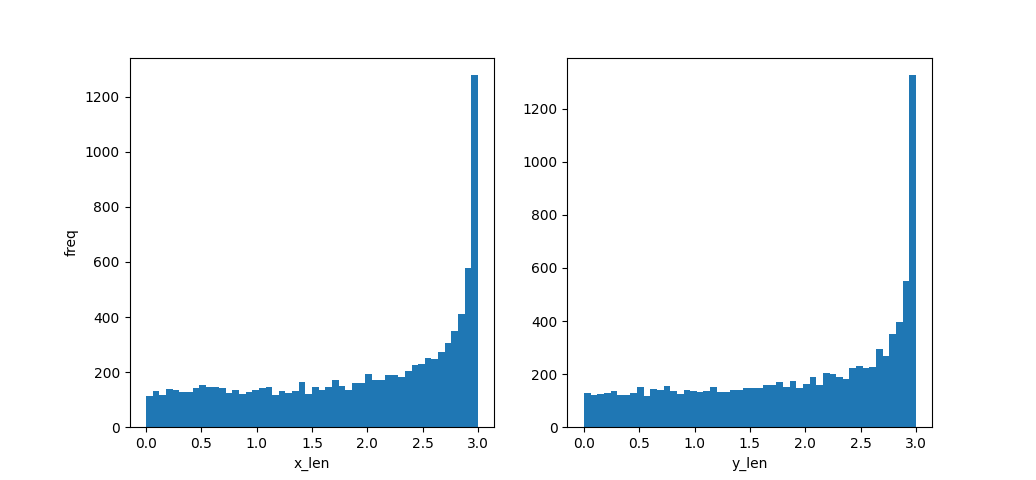
まずは、クラス①の場合です。
つづいて、クラス②の場合です。
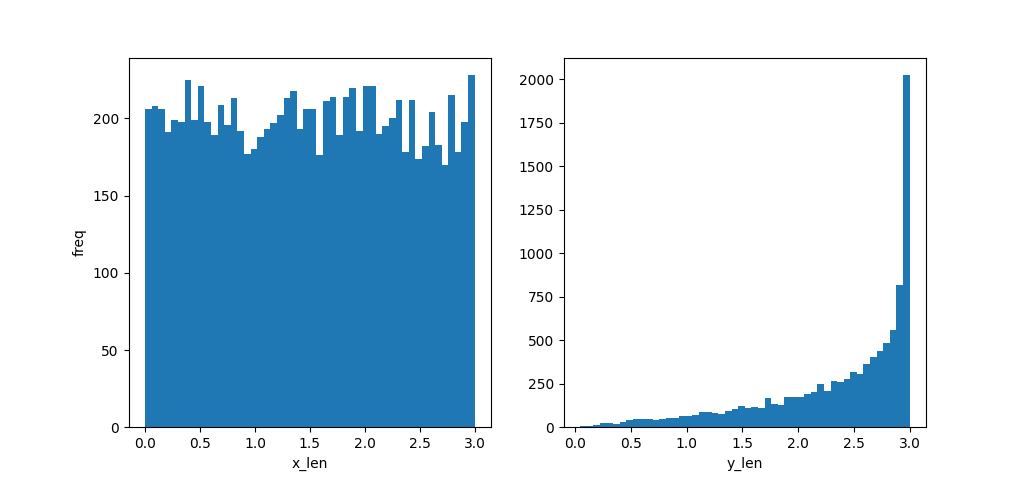
「x」「y」でも違いは一目瞭然ですね。
クラス①の場合は、「x」「y」ともに同じような分布を示しています。
一方で、クラス②の場合は、「x」「y」で異なったグラフになりました。
「x」は均一に分散していますが、「y」は偏ったグラフになっています。
この結果は、「統計的手法」で出した結論と同じですね。
結論として、クラス②は「x」を平均的に扱ったのが失敗だったという事です。
6.散布図で遊ぼう!
検証は終わりましたが、もう少し遊んでみましょう。
ここまで、「x」と「y」は絶対値で出してきました。
つぎは、絶対値とせず(=+とーをもつ値)に「x」と「y」で散布図を描写してみます。
ついでに、グラフの色を変えて遊んでみましょう。
なお、グラフの色は、matplotlib公式:List of named colorsで確認できます。
では、プログラムを書いていきましょう。最後なので、全部乗せします。
先に作ったヒストグラム表示はここでは描写しないのでコメントアウトしています。
from matplotlib import pyplot as plt
import statistics
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0 , x_ep = 1, y_ep = 0):
super().__init__(n_len, x_lim, y_lim, x_posi, y_posi, theta) #x_ep、y_ep以外は親クラスのまま super()で呼び出し
self.x_ep = x_ep #x末端座標定義
self.y_ep = y_ep #y末端座標定義
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
cos_theta = x_ep_len/self.n_len # cosθ = x座標距離 / 針長さl
theta_dg = math.degrees(math.acos(cos_theta)) #cosθ > θ(ラジアン) > θ(degree)
self.theta = y_ep_pm * theta_dg # 180°以上ならy_ep_pmは-1
if self.theta < 0:
self.theta +=360 #180°以上なら、-theta+360
def endpoint(self, xy = 'y'):
x_ep = self.x_ep #x_epはthrowで計算済み
y_ep = self.y_ep #y_epはthrowで計算済み
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
theta_list = [] #角度θのリスト
len_x_list = [] #x座標間距離のリスト
len_y_list = [] #y座標間距離のリスト
len_x_list_not_abs = [] #x座標間距離のリスト 絶対値なし
len_y_list_not_abs = [] #y座標間距離のリスト 絶対値なし
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
theta_list.append(needle.theta) #角度θのリスト出力
len_x = abs(needle.x_posi - needle.endpoint(xy='x')) #x座標間距離計算
len_y = abs(needle.y_posi - needle.endpoint(xy='y')) #x座標間距離計算
len_x_list.append(len_x) #x座標間距離のリスト出力
len_y_list.append(len_y) #y座標間距離のリスト出力
len_x_not_abs = needle.endpoint(xy='x') - needle.x_posi #x座標間距離計算
len_y_not_abs = needle.endpoint(xy='y') - needle.y_posi #x座標間距離計算
len_x_list_not_abs .append(len_x_not_abs ) #x座標間距離のリスト出力
len_y_list_not_abs .append(len_y_not_abs ) #y座標間距離のリスト出力
num += 1
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
buffon_main(para.t_val, para.l_val, para.n_val)
v_list = ['θ', 'x_len', 'y_len']
v_output_list = [theta_list, len_x_list, len_y_list]
for (v, i) in zip(v_list, v_output_list):
ave = statistics.mean(i) #平均値
med = statistics.median(i) #中央値
std = statistics.stdev(i) #標準偏差
print(f'{v} : 平均{ave:.3f}, 中央値{med:.3f}, 標準偏差{std:.3f}')
""" plt.hist(theta_list, bins=360) #θのヒストグラム 1°ごとに分割
plt.xlabel('θ') #x軸ラベル θ
plt.ylabel('freq') #y軸ラベル freq
plt.show() #グラフ描写 """
""" fig = plt.figure() #描写エリア設定
ax= fig.subplots(1, 2) #横並びに2つのグラフ設定
ax[0].hist(len_x_list, bins = 50) #グラフ1にxのグラフ、50分割
ax[0].set_xlabel('x_len') #グラフ1のx軸ラベル変更
ax[0].set_ylabel('freq') #グラフ1のy軸ラベル変更
ax[1].hist(len_y_list, bins = 50) #グラフ2にxのグラフ、50分割
ax[1].set_xlabel('y_len') #グラフ2のx軸ラベル変更
plt.show() #グラフ描写 """
fig = plt.figure() #描写エリア設定
ax = fig.subplots(1, 2) #横並びに2つのグラフ設定
ax[0].scatter(len_x_list_not_abs , len_y_list_not_abs, c='lime') #グラフ1にx、yの散布図 cで色指定
ax[0].set_xlabel('x_len') #グラフ1のx軸ラベル変更
ax[0].set_ylabel('y_len') #グラフ1のy軸ラベル変更
ax[1].scatter(theta_list, len_x_list_not_abs , c='gold', label ='x_len') #グラフ2にθ、xの散布図
ax[1].scatter(theta_list, len_y_list_not_abs, c='mediumslateblue', label ='y_len') #グラフ2にθ、yの散布図
ax[1].set_xlabel('θ') #グラフ2のx軸ラベル変更
ax[1].set_ylabel('x_len , y_len') #グラフ2のy軸ラベル変更
ax[1].legend() #凡例表示
plt.show()
色は、適当に選びました。
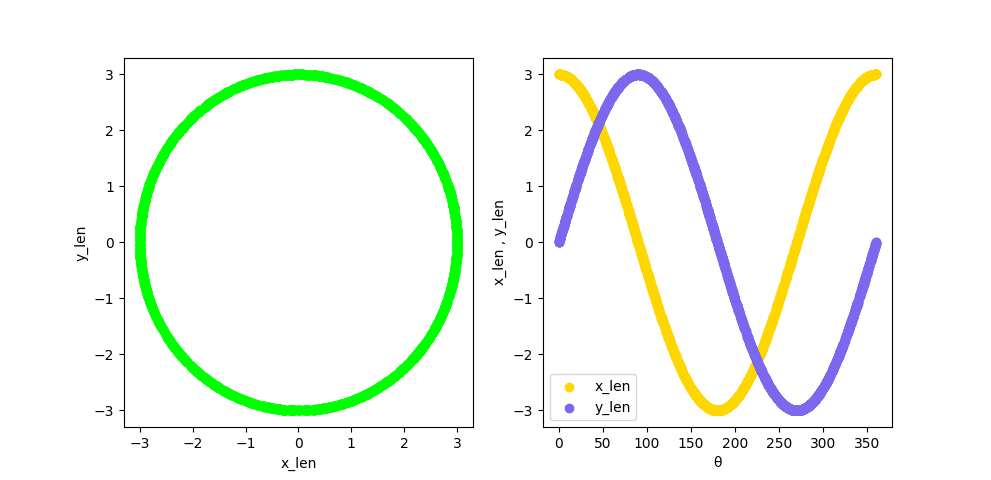
では、クラス①の場合から実行してみます。今回はあえて試行回数を2000回にしてみます。
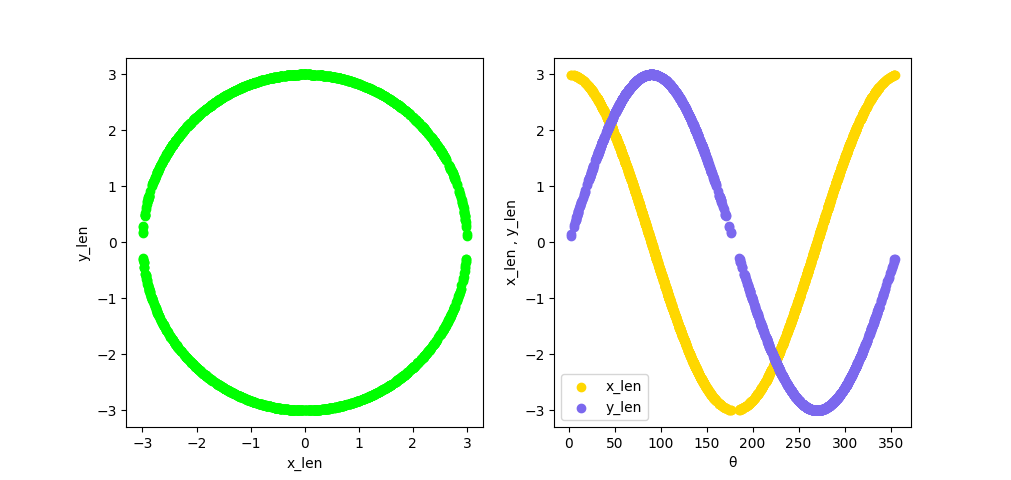
次はクラス②の場合です。こちらも試行回数を2000回にしてます。
まず、きれいな色で書けました!!
どちらも、「x」と「y」の散布図は、円形になっています。
しかし、クラス②のほうでは、「y_len = 0」付近で途切れています。
これは、ヒストグラムで検証した結果と一致していますね。
もう一つのグラフでは、まず、一つのエリアに2つのグラフが描けており、凡例表示もできています。
「x_len」の方は、sinカーブ、「y_len」の方はcosカーブが描けています。
こちらもクラス②のほうでは、「y_len = 0」付近で途切れています。
これにて検証終了!!
7.少し補足 ~Jupyter Notebookの場合~
ここまでは、通常どおりコードを書いて、ターミナル(コマンドプロンプト等)で実行するというやり方で書いてきました。
実際は、グラフ描写等を行う場合は、AnacondaについてくるJupyter Notebookで記載する場合が多いようです。
Jupyter Notebookの場合、このように記載するようです。
冒頭に%matplotlib inline、グラフ描写の最後に「;」です。
%matplotlib inline
from matplotlib import pyplot as plt
import statistics
import random
import math
~~~~~略~~~~~
plt.hist(theta_list, bins=360) #θのヒストグラム 1°ごとに分割
plt.xlabel('θ') #x軸ラベル θ
plt.ylabel('freq'); #y軸ラベル freq補足終了!!
さて、今回、統計とグラフを活用して、何がダメであったかを検証することが出来ました。
次回は、もう少しグラフで遊んでみます。
To Be Continued : ビュフォンの針を落とす ep4
PyQさんで勉強中!




コメント