
前回はうまくいかなかったなぁ
ちょっとアプローチを変えてやってみよう!
記事①:pV=nRT 単位換算地獄 ~気体の状態方程式をPythonで! ep 1~
記事②:実在気体をPythonで解く~気体の状態方程式をPythonで! ep 2~
前回、実在気体の状態方程式にチャレンジして大爆死してしまいました。
プログラムに関しては、始めにイメージしていたものができましたが、動かしてみると出てきた値が発散してしまいました。
あの後、ふとした瞬間(仕事中・・・集中してないのがバレる)に解決できそうな方法を思い付いたので、凝りもせず再チャレンジしてみます!
(2021年3月11日:学習開始20日目)
みんな、オラに元気をほんのちょっと分けてくれ!!
今回は実在気体への復讐します。「偉大なる復讐」ということでThe Heavyの「Great Vengeance and Furious Fire」から「Coleen」とともに戦っていきます。
日本では、CMで使われたこっちの「Same Ol’」の方が有名ですね。(どっちも曲名から公式YouTubeに飛びます。)
先に言っておきますが、実在気体の状態方程式を完成させます。
1.前回の振り返り(と反省)
冒頭にかいたとおり、前回は実存気体を状態方程式にチャレンジして失敗しました。
考え方は、実際のデータをいくつかインプットして計算を繰り返し、状態方程式を補正してやればいい感じになるのでは?という事で進めていきました。
この「計算を繰り返す」というところが、プログラミングの利点の一つだと思いますので、チャレンジしてみたわけです。
何がダメだったのか?やったことを見直してみました。
①:実存気体へのチャレンジ
→OKとしましょう。出来たらなんかすごそうですし。
②:大まかなアプローチ
過去に考案された実存気体の状態方程式のうち「ビリアル方程式」を選定し計算する。
ビリアル方程式は、以下のような方程式です。
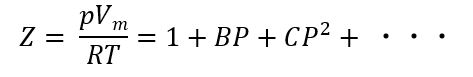
これを選定した理由は補正項が無限にあるので、最終的には収束すると考えたからです。
プログラミングと相性が良いと考えました。
→この辺りから、正しいかどうか微妙なところです。方程式の選定は見直しの余地ありです。
(※結果的に今回もこの式を活用しています。)
③:具体的なアプローチ
実際のデータをインプットして、計算を行う。
計算の手順は以下の流れで行った。
(1)データをインプットして計算できる形に単位合わせした
(2)ビリアル方程式のC以下を無視、それぞれインプットしたデータからBを計算
(3)データごとにBが計算できるので、それぞれの値から平均値Baveを計算
(4)元の式のBにBaveを代入して、実データのp、TからV(cal)を計算
(5)実データのV(real)と計算ででてきたV(cal)を比較、10%の誤差なら終了
(6)V(real)とV(cal)の差が大きい場合は、Cの計算にうつる。
(7)D以下を無視、BはBaveとしてCの計算を行う。
この結果、計算すればするほど実データと計算値が乖離してしまった・・・
→このアプローチが完全に失敗!
④:プログラミング
詳細は省略しますが、プログラムはおおむね③のアプローチ通りの動きができました。
→プログラミングは成功!ただしアプローチをミスったので、あんなことに・・・
やはり②と③に問題がありそうです。
(※実はもう1つ問題点があります。インプットする実データとして「水蒸気(水)」を用いた点です。水は、水素結合をするため分子間の相互作用が強く、理想気体との乖離が大きい気体です。つまり、理想気体から補正するには適していません。今回、ネットで拾えるのが水蒸気しかなかったのでこれを使いましたが、例えばヘリウムとかであればもっとうまくいったかもしれません。)
2.作戦会議~復讐への道~
ここまで振り返ってみて見直すべき点は2つです。
1つが「方程式の選定」、もう一つが「計算のアプローチ」です。
「方程式の選定」については、その後いろいろ調べましたが、良さそうなものが見当たりません。
たとえば、最も有名なファンデルワールスの状態方程式を見てみましょう。
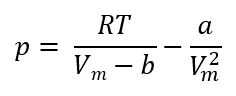
この、aとbが理想気体からの補正項になります。
ここで、インプットする式を1つとした場合、どのようになるでしょうか?
データが1つの場合、aとbは決めることができず、a =(なにかしらの数字)bとなります。
つぎにデータ2つの場合、aとbはそれぞれ具体的な値が決まります。
さらにデータが3つの場合、うまくいけばaとbはだいたい決めることができます。
例えば3データのうち2つを使って算出したa、bと、ほかの2つのデータから算出したa、bがおおむね同じ値であればOKです。
ただし、これが全く異なる値になれば、「解なし」となってしまいます。
つまり、インプットするデータが良ければ(理想気体に近ければ)、aとbは決まるということです。
さらにさらにデータが4つ以上の場合はどうなるでしょうか?
この場合、データ3つの場合と同じようにすれば、aとbの検証はできますが、aとbの値が落ち着く可能性はデータが増えれば増えるほど絶望的になっていきます。
「データが増えるほど答えが遠のく」、これはプログラミングと相性が悪い、悪すぎます。
このような式を使う場合、機械的に計算するのではなく、物理的に妥当な値を考える必要があるということです。
ここでは、ファンデルワールスの状態方程式を見てみましたが、補正する係数の数が決まっているものはいずれも同じ問題にぶつかります。
う~ん、やはりビリアル方程式に代わるものは見つかりません。少しおいて計算のアプローチに目を向けましょう。
「計算のアプローチ」は何がマズかったのでしょうか?考えてみましょう。
実は、ファンデルワールスの検証に大きなヒントがあったのです。
それは、「インプットするデータの数=係数の場合、特殊な場合を除いて係数は1つに決まる」ということです。
ここでいう、「特殊な場合」というのは、p=1、V=1、T=1とp=2、v=2、T=2のような等しい倍率で増減するデータを用いた場合です。このようなケースは実データではほぼないと思われるので、考えなくても良さそうです。
ということは、、、
「インプットデータ数 = ビリアル方程式の係数の数」
とすれば、解が求まるはずです。
おー光が見えてきました。
前回は、まずBを決めてBを固定、次にCを決めてCを固定、Dを決めてDを固定・・・としていましたが、これをやったことで、BのズレがCに、CのズレがDにというようになってしまいました。
今回は、5データなら、B、C、D、E、Fをすべてのデータから一気に決めるという事になります。
このアプローチでやってみます!
3.フローチャート
いつもどおり、フローチャートから書いていきます。
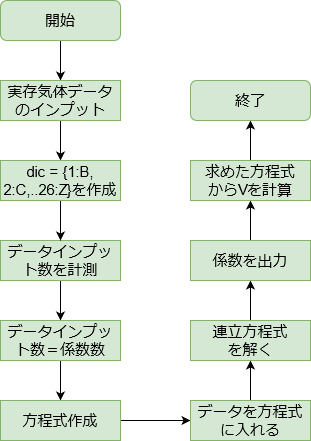
フローチャートは簡単ですね。
しかし、ひとつヤバいのがあります。「連立方程式を解く」これです。
2係数、3係数ならかけそうですが、10係数、n係数ってどうするのか・・・
調べてみると、「連立方程式を解いてしまえるモジュール」があるようです。
pythonまじpython!!!!
こちらのページを参考にさせてもらいました。(【Python入門】Numpy行列やSympyで連立方程式を簡単に解く方法)
こちらではNumpyとSympyという2つの方法が紹介されています。
詳しくはリンク先のページをみてもらった方が正確かつ分かりやすいですが、簡単にいうと
2x + 3y = 16、x + 7y = 19という式があった場合に、
「Numpy」は左辺のリスト[[2,3][1,7]]と右辺のリスト[16,19]で計算する方法
「Sympy」はxとyを定義して2x + 3y = 16、x + 7y = 19の式から計算する方法
ということです。
今回は、変数の数がインプットするデータ数により異なるので、Numpyの方が適していると判断しました。Numpyを使っていきます。さて行きましょう。
4.プログラムを書いていこう、の前にNumpyってどんなん?
大体方針も定まったので、プログラムを書いていきましょう。
その前にNumpyを使ってみます。いったん無茶な値でも大丈夫か見てみます。
from numpy.linalg import solve
left = [[0.0003, 0.02],
[8*10**-2, 10**6]]
right = [1, 80000]
print(solve(left, right))これは、0.0003x + 0.02 y = 1, 8x10-2 + 106= 80000で計算したものです。
結果、このようになりました。
ModuleNotFoundError: No module named 'numpy'ModuleNotFoundError: No module named 'numpy'なーーーにーーーー!numpyモジュールがない、だと?
どうやら、Numpyはrandomのようにもともと使えるものではなく、インストールする必要があるらしいです。
ここでNumpyをインストールしても良いのですが、私は「Anaconda」をインストールすることにしました。
「Anaconda」はNumpyをはじめ、めちゃめちゃたくさんのデータサイエンスや機械学習などに使えるモジュールを詰め込んでpythonを動かせるソフトです。(説明あってるのか?)
こちらのページAnaconda を Windows にインストールする手順を参考にインストールしました。
(※すでにPythonが入っていて、Anacondaを入れると不具合があることもあるそうです。ご注意ください。私は問題ありませんでした。)
さて「Anaconda」をインストールしたので、これでやってみましょう。
なお、これ以降は基本的には「Anaconda」を使用することとします。気づかずノーマルPythonでは入っていないモジュールを使用するかもしれませんがご容赦ください。
で、先ほどのプログラムを動かしてみました。
[3.32801775e+03 7.97337586e-02]よし!結果が返ってきました。多分あっているでしょう。では4変数ではどうでしょうか?
これを動かしてみます。4変数なので、左辺は4つの数字リストが4つ、右辺は4つの数字リストとなっています。
from numpy.linalg import solve
left = [[0.0003, 0.02, 4848642, 489],
[8*10**-2, 10**6, 958, 8852],
[46546, 56498, 48, 77546],
[48562674, 781631, 89, 226]]
right = [1, 80000,8940, 10**-3]
print(solve(left, right))結果はこうなりました。
[-1.27961092e-03 7.94853188e-02 -5.65803452e-06 5.81435470e-02]適当な値でもやはり、1つの解がきまりました。これは使えますね。
連立方程式がと解けることが分かりましたので、左辺と右辺に分けるような形に持っていけばよいですね。
一度、元のビリアルの式に戻りましょう。今回は5個のデータをインプットすることを考えます。
この場合、変数も5個になるので、解く式は以下です。

ここでP、Vm、Tは実データに基づき数字が入るので、Numpyではこのような形にすればよいです。
left = [[p, p2 ,p3,p4,p5], [データ2], [データ3], [データ4], [データ5]]
right = [z-1, データ2, データ3, データ4, データ5]
ここでデータ2のように書いているのは、それぞれ1番先頭のような形で用いる実データが異なるものを指します。(説明下手くそかよ、なんとなく言いたいことは分かりますよね?お察しください。)
Numpyでの連立方程式が分かったので、ついにプログラムを書いていきます。
5.プログラムを書いていこう
初めからプログラムを書いていきましょう。
ただし、なるべく前回のものを流用したいと思います。
データのインプットですが、前回と同じものを使います。
| 温度(℃) | 圧力(MPa) | 比容積 (m3/kg) | |
| ① | 120 | 0.19853 | 0.8919 |
| ② | 170 | 0.7917 | 0.2428 |
| ③ | 220 | 2.318 | 0.08619 |
| ④ | 270 | 5.499 | 0.03564 |
| ⑤ | 320 | 11.274 | 0.015488 |
これを「steam.csv」として読み込ませます。で、それぞれのデータを温度をK、圧力をPa、比容積をm3/molに変換します。データの数をカウントして辞書型のリストに入れていきます。
ここまでは前回と全く同じですので、詳しい説明は略しますが、プログラムは以下です。
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dicこれで出てくるデータは
{0:[データ①のT, データ①のp, データ①のVm], 1:[データ②のT, データ②のp, データ②のVm], ・・・}のようになっていました。
次に、辞書形式のデータで{1:B, 2:C,・・・25:Z}を作成します。これも前回と同じですので、プログラムのみ記載します。ただし今回は、defで関数として定義しました。
結果はうまく書けるのが分かっているので略します。
def alphabet_list():#数字:アルファベット辞書作成
num_ab_dic = {}
for dic_num in range(1,26):
num_ab_dic[dic_num] = chr(ord('B')- 1 + dic_num)
return num_ab_dic実は今回はこのB~Zを作る必要はなく、これに則ると26個のデータしかインプットできなくなります。ただ、まずは、簡略化のために前回を踏襲します。
次のデータインプット数を計測も前回やっていて、データの辞書型のリストをdata_dicとすると以下で表せます。
len(data_dic)ここまでは、前回と同じでしたが、ここからは新たにプログラムを書く必要があります。
まず、右辺と左辺のリストを作成します。ここもdef関数を定義して書いてみます。この関数では連立方程式を解くところまで書きましょう。
イメージは、まず空の右辺、左辺リストを作成して、その後、インプットするデータをforで一つずつ処理して空のリストに加えていくような感じです。
まずは、右辺を作るところまで書いてみます。
def solve_renritsu(con_dat_dic):#con_dat_dicを入れれば係数が変える関数
from numpy.linalg import solve #numpyのsolveをインポート
right_list =[]#右辺の空リスト
left_list =[]#左辺の空リスト
for num, st_list in con_dat_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
z = (pres*volu) / (R*temp) #Z=PV/RT
right = z-1 # right = pv/rt - 1
right_list.append(right)#right_list=[z1-1,z2-1・・・]これで、Z-1 = pV/RT -1として、
right_list = [Z(データ①)-1, Z(データ②)-1, Z(データ③)-1・・・]となります。
続いて、左辺を作っていきます。
左辺はleft_list = [[データ①の左辺の係数], [データ②の左辺の係数]・・・]となり、リストの中にリストが入ったようにする必要があります。これを踏まえて続きを作ります。
def solve_renritsu(con_dat_dic):#con_dat_dicを入れれば係数が変える関数
~~~~略~~~~
right_list.append(right)#right_list=[z1-1,z2-1・・・]
left = []#1データの左辺(pB+p^2C+p^3D・・・)
for p_num in list(range(1, 1+len(con_dat_dic))):#p_num = 1~データ
left.append(pres**p_num) #left = [p, p^2, p^3 ・・・]
left_list.append(left) #left_list = [[left1], [left2]・・・]ここで注意が必要なのがfor構文のところです。
p_numのところは1、2、3・・・(データの数=ここでは5)としています。
leftは[p, p2 ,p3,p4,p5]のリストを作りたいので、p**(p_num)としています。
これで、左辺と右辺が用意できました。
次は、連立方程式を解くところです。さらに答えを出力するところまで書いていきます。
ここではB=XXX、C=YYYのように出力したいので、英語リストを呼び出します。
これらを踏まえて以下のようになりました。
def solve_renritsu(con_dat_dic):#con_dat_dicを入れれば係数が変える関数
from numpy.linalg import solve #numpyのsolveをインポート
right_list =[]#右辺の空リスト
left_list =[]#左辺の空リスト
for num, st_list in con_dat_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
z = (pres*volu) / (R*temp) #Z=PV/RT
right = z-1 # right = pv/rt - 1
right_list.append(right)#right_list=[z1-1,z2-1・・・]
left = []#1データの左辺(pB+p^2C+p^3D・・・)
for p_num in list(range(1, 1+len(con_dat_dic))):#p_num = 1~データ
left.append(pres**p_num) #left = [p, p^2, p^3 ・・・]
left_list.append(left) #left_list = [[left1], [left2]・・・]
solve_list = solve(left_list, right_list)#連立方程式の解
ab_list = alphabet_list()#数字:アルファベット辞書呼び出し
for ab_num in list(range(1, 1+len(con_dat_dic))):
alp = ab_list[ab_num]
sol = solve_list[ab_num-1]
print(f'{alp} = {sol:.5e} ')
return(solve_list)ここまでを合算して、プログラムを動かしてみました。
data_dic = list_input()
solve_keisu = solve_renritsu(data_dic)
結果は以下です。
(後ですべてを合算するので、ここではプログラムは略して結果のみ)
B = -1.44102e-07
C = 1.24098e-13
D = -5.47952e-20
E = 8.89451e-27
F = -4.37502e-34行けました!!!!前回はこの時点で発散していたので、大きな成長です。
次は、算出された値が正しいかどうかを検証します。
前回同様、実データのpとTからVmを求めて、実データのVmと比較していきます。
一度、元のビリアルの式を見直してみましょう。
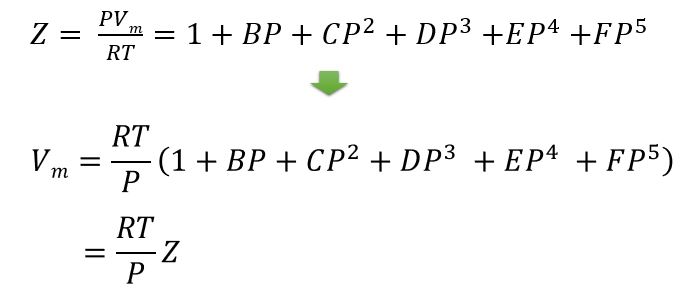
Zの中身をfor構文で書いていき、計算すればよいですね。
B、C、Dは先ほど求めた係数のsolve_list[0], solve_list[1], solve_list[2]とかけます。
ここも、defで関数として書いていきます。また、ここでは、「データリスト」と「算出した係数リスト」を2変数とした関数にします。
では、いきましょう。
def kensyou(c_dat_dic, s_list):
def kensyou(c_dat_dic, s_list):#c_dat_dicとs_listを入れれば検証できる関数
for num_2, st_list_2 in c_dat_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
z_2 = 1 #Z_2 = 1 + BP + BP^2 +・・・
for y in list(range(0, len(c_dat_dic))): #y = 0~データ数-1
z_2 += s_list[y]*(pres**(y+1)) #Z_2にs_list[0]*p**1, s_list[1]*p**2・・・を加える。
Vb = (z_2)*(R*temp)/pres #ビリアルの状態方程式から計算
print(f'{num_2} : 実データのVm:{volu:.5f} 理想気体のVm:{vid:.5f} ビリアルの状態方程式から求まるのVm:{Vb:.5f}')ここまでをすべてまとめると次のようになります。
また、最後にはそれぞれ作った関数を動かすプログラムを入れています。
R = 8.314462 #気体定数[J/K・mol]
def alphabet_list():#数字:アルファベット辞書作成
num_ab_dic = {}
for dic_num in range(1,26):
num_ab_dic[dic_num] = chr(ord('B')- 1 + dic_num)
return num_ab_dic
def list_input():
list_num = 0 #データ数カウント
conv_data_dic = {}
with open('C:/Users/XXXX/YYYY/steam.csv', 'r', encoding = 'utf-8') as f:
for row in f: #steam.csvを開く
data_list = row.strip().split(',')#改行なくし #','で区切る
temp_c = float(data_list[0]) #温度C
pres_mpa = float(data_list[1]) #圧力MPa
vol_kg = float(data_list[2]) #体積m3/kg
list_t = temp_c + 273.15 #温度T
list_p = pres_mpa *1000000 #圧力Pa
list_v = vol_kg *0.001 * 18.01528 #体積m3/mol
conv_data_dic[list_num] = [list_t, list_p, list_v]
list_num += 1
return conv_data_dic
def solve_renritsu(con_dat_dic):#con_dat_dicを入れれば係数が変える関数
from numpy.linalg import solve #numpyのsolveをインポート
right_list =[]#右辺の空リスト
left_list =[]#左辺の空リスト
for num, st_list in con_dat_dic.items():
temp = st_list[0]
pres = st_list[1]
volu = st_list[2]
z = (pres*volu) / (R*temp) #Z=PV/RT
right = z-1 # right = pv/rt - 1
right_list.append(right)#right_list=[z1-1,z2-1・・・]
left = []#1データの左辺(pB+p^2C+p^3D・・・)
for p_num in list(range(1, 1+len(con_dat_dic))):#p_num = 1~データ
left.append(pres**p_num) #left = [p, p^2, p^3 ・・・]
left_list.append(left) #left_list = [[left1], [left2]・・・]
solve_list = solve(left_list, right_list)#連立方程式の解
ab_list = alphabet_list()#数字:アルファベット辞書呼び出し
for ab_num in list(range(1, 1+len(con_dat_dic))):
alp = ab_list[ab_num]
sol = solve_list[ab_num-1]
print(f'{alp} = {sol:.5e} ')
return(solve_list)
def kensyou(c_dat_dic, s_list):#c_dat_dicとs_listを入れれば検証できる関数
for num_2, st_list_2 in c_dat_dic.items():
temp = st_list_2[0]
pres = st_list_2[1]
volu = st_list_2[2]
vid= (R*temp)/pres #理想気体として計算
z_2 = 1 #Z_2 = 1 + BP + BP^2 +・・・
for y in list(range(0, len(c_dat_dic))): #y = 0~データ数-1
z_2 += s_list[y]*(pres**(y+1)) #Z_2にs_list[0]*p**1, s_list[1]*p**2・・・を加える。
Vb = (z_2)*(R*temp)/pres #ビリアルの状態方程式から計算
print(f'{num_2} : 実データのVm:{volu:.5f} 理想気体のVm:{vid:.5f} ビリアルの状態方程式から求まるのVm:{Vb:.5f}')
data_dic = list_input()
solve_keisu = solve_renritsu(data_dic)
kensyou(data_dic, solve_keisu)では、動かしてみた結果です。
B = -1.44102e-07
C = 1.24098e-13
D = -5.47952e-20
E = 8.89451e-27
F = -4.37502e-34
0 : 実データのVm:0.01607 理想気体のVm:0.01647 ビリアルの状態方程式から求まるのVm:0.01607
1 : 実データのVm:0.00437 理想気体のVm:0.00465 ビリアルの状態方程式から求まるのVm:0.00437
2 : 実データのVm:0.00155 理想気体のVm:0.00177 ビリアルの状態方程式から求まるのVm:0.00155
3 : 実データのVm:0.00064 理想気体のVm:0.00082 ビリアルの状態方程式から求まるのVm:0.00064
4 : 実データのVm:0.00028 理想気体のVm:0.00044 ビリアルの状態方程式から求まるのVm:0.00028よっしゃーーーーーーーー!!!!!
すべてのデータで実データ=方程式から求まるVmとなっています。
実在気体の状態方程式を完成させることが出来ました。
ついに実在気体の状態方程式に復讐を果たすことが出来ました。
いや~長かった~。というか、これ我ながらなかなか凄いものが出来たんじゃない?
次回、この方程式の妥当性をもう少し調べます。
To Be Continued : 気体の状態方程式をPythonで! episode 4
PyQさんで勉強中!





コメント