
「ビュフォンの針」のシミュレーションで円周率が出せた!!
けど、円周率出すのに、sinθ使っちゃったのがなぁ・・
記事①:Pythonで円周率を求めよう ~ビュフォンの針を落とす ep1~
前回は、「ビュフォンの針」の問題をシミュレーションにより解きました。
それなりにできたのですが、問題はsinθを使って解決しているところです。
今回、まずここを解決していきましょう。
(2021年4月17日:学習開始57日目 PyQさんで勉強中!)
今回も、引き続き「ビュフォンの針」と戦います。
前回に引き続き「針」に関わる曲を聴きながらやっていきます。
前とは一転、メロデス=メロディックデスメタルの雄 Children of Bodom の超名盤 「Hate Crew Deathroll」から強力なパンチを食らわせる曲「Needled 24 / 7」を聞いて、テンションを挙げていきましょう!!(曲名から公式YouTubeに飛びます。)
さてさて、やっていきましょう!
(プログラムは最後に完成していますが、今回爆死回です!!)
1.前回の振り返りと今回やりたい事
冒頭でも書いていますが、前回、「ビュフォンの針」のシミュレーションにより、円周率をそこそこ求めることが出来ました。
まずは、簡単に「ビュフォンの針」の問題を振り返りましょう。
詳細は前回の記事にあるので省略しますが、内容は以下です。
①:間隔tで平行線が描かれている床を用意します。
②:長さl(エル)の針を床に落とします。(針は床に刺さらずに倒れるものとします。)
③:床の平行線と針が交差する確率を求めます。
で、t > lの場合、針と床の線が交差する確率は、以下のようになり円周率が現れます。

で、前回は以下の図をもとに考えました。
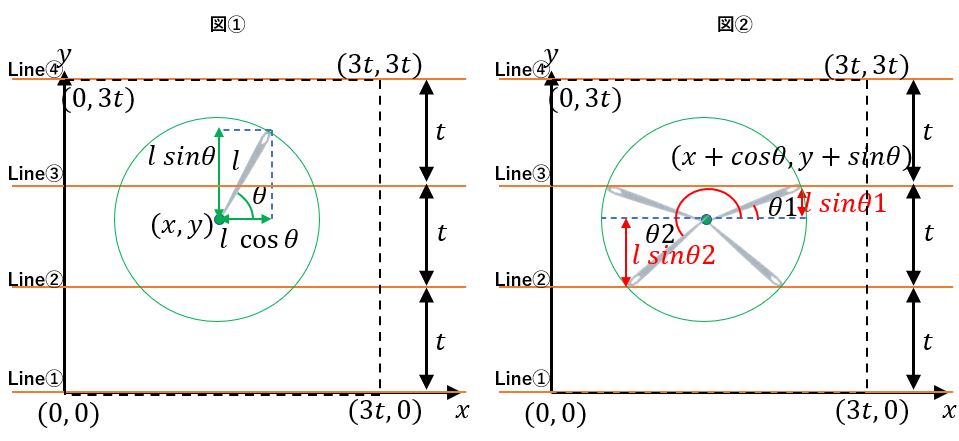
要は、針先のポイント(x, y)と平行線との角度θから、平行線と重なるかどうかを判定しました。
上に記載した、「ビュフォンの針」のルールから考えると、特に問題はありません。
しかし、最終的に円周率を出したいので、その算出の途中にθを使うのはちょっと微妙です。
今回は、確率の算出に角度θを使わずに求めてみましょう!!
2.作戦会議
θを使わずに、問題を解いていくと決めました。
では、どのように解決すれば良いのでしょうか?
やること自体は、「ビュフォンの針」の内容から変わりません。
①「針を落とす」=「針先を決める」→「針末端座標を決める」
②平行線と交差しているかを判定する。
③繰り返し実行し、確率を算出する。
前回は、①の「針末端座標を決める」ところにθをつかう必要がありました。
そのため「針を落とす」ところでθを決定していました。
ここを改善する必要がありそうです。
では、「針末端座標」をどのように決めればよいでしょうか?
図で考えてみます。
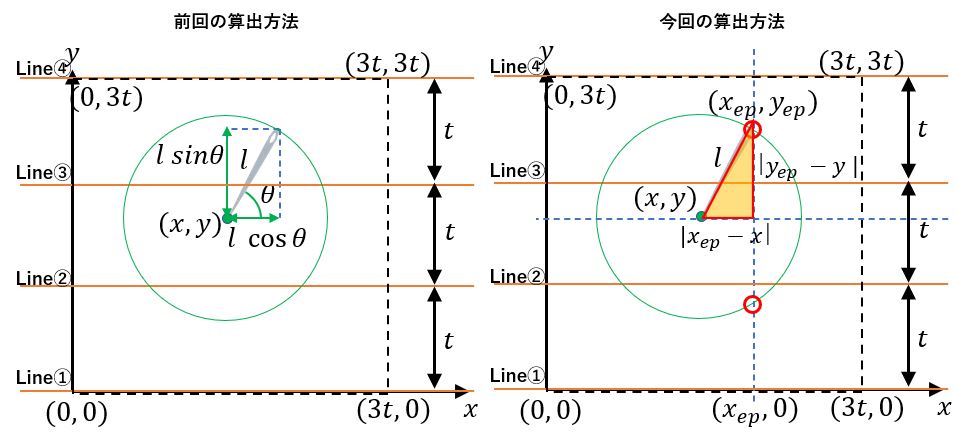
前回は、「針先座標(x, y)」、「針の長さl」、「角度θ」から「針末端座標 (x_ep, y_ep)を求めていました。
今回は、「針先座標(x, y)」、「針の長さl」および「針末端x座標 x_ep 」から、「針末端y座標 y_ep 」を求める、というやり方を考えたいと思います。
もうひとつ、プログラムの書き方についてです。
前回作成した、class「ニードル」を「継承」して新たな子クラスを作成したいと思います。
継承をめちゃめちゃ雑に言うと、「元のclass(=親クラス)と同じ機能を別のclass(=子クラス)」を作って、「子クラスの変数、関数をいい感じに変える」って感じです。
ではやっていきましょう。
3.プログラムを書いていこう① ~改変ポイント整理~
ではプログラムを書いていきましょう。
クラスを継承して新たなクラスを作成します。
では、前回のプログラムを振り返りましょう。前回記事からclass「needle」部分を抜粋します。
import random
import math
~~~~~略~~~~~
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
~~~~~略~~~~~
では、新たに作成するclass(=子クラス)に持たせたい機能(=親クラスからの改変ポイント)を考えていきましょう。
この「改変」ですが、「オーバーライド」といいます。かっけぇ・・・。
子クラスの名前はclass「needle_not_theta」とします。
改変ポイント①:クラス変数x_ep、y_epの導入
親class「needle」では、クラス変数として「n_len」「x_lim」「y_lim」「x_posi」「y_posi」「theta」を持っていました。
針の末端座標を意味する「x_ep」と「y_ep」は「endpoint」関数の中で算出されています。
子class「needle_not_theta」では、「x_ep」と「y_ep」をクラス変数として導入することにします。理由は、次の関数にかかわります。
改変ポイント②:throw関数でθを変えずにx_epを決める。y_epとθを計算する。
親class「needle」ではthrow関数で、針の先端位置「x_posi」「y_posi」と角度「theta」をランダムで決めました。
子class「needle_not_theta」では、針の先端位置「x_posi」「y_posi」と針の末端位置「x_ep」をランダムで決めます。図から考えてみましょう。
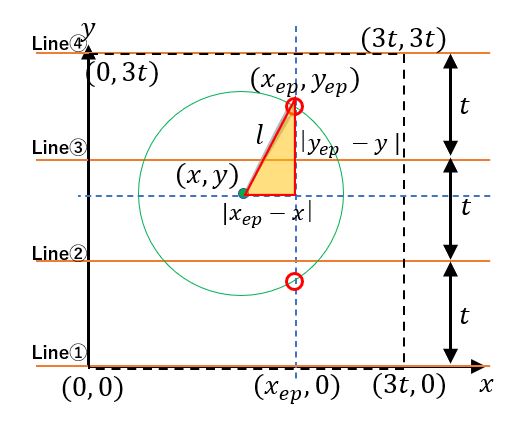
「x_ep」は「x_posi」を中心として長さlを持ちます。
つまり、「x_ep」の座標は、「x_posi ー l ~ x_posi + l」の間に収まります。
針の末端位置「y_ep」を計算します。
三平方の定理を使えば計算できます。
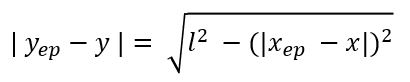
ここから、「y_ep」を算出できます。
しかし、この時点では「y_ep」の取りうる箇所は2カ所存在します。(図の赤丸位置)
そのため、y_ep = y + |y_ep – y| か、 y_ep = y – |y_ep – y|を選択する必要があります。
上の式をみると、一カ所+かーを選択すれば良さそうです。
続いて「θ」を算出します。
「x_ep」と「y_ep」「l」が決まっているので、ここから「θ」が計算できますね。
三角関数のが逆関数arccosから算出できます。(sin、tanでは無くcosを選択した理由は後述)
ここでも解決すべき問題があります。0~360°の中に同じcosを取る角度が2カ所あります。
この解決を考えた結果、cosで計算しています。
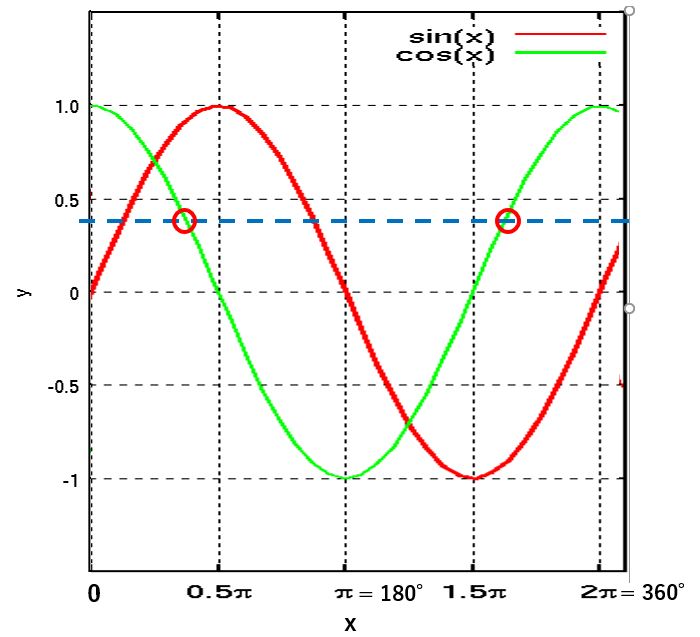
θが180°以下、 つまりy_ep = y + |y_ep – y|の場合は、arcosで計算できます。
θが180°以上、 つまりy_ep = y ー |y_ep – y|の場合は、360° – arccosで計算できます。
改変ポイント③:endpoint関数でx_ep、y_epを計算しない
親class「needle」はここで針の末端位置「x_ep」「y_ep」を計算しました。
子class「needle_not_theta」ではすでに計算済みですので、値を返すだけにします。
改変ポイント④:y_change関数をここまでの改変に合わせて調整する
基本的に親class「needle」と子class「needle_not_theta」でやることは同じです。
これまでの改変に合わせて調整します。
ではやっていきましょう。
4.プログラムを書いていこう② ~子クラス作成~
改変ポイントを改めてまとめてみましょう。

上から処理していきましょう。
改変ポイント①:クラス変数x_ep、y_epの導入
ここで子class「needle_not_theta」を作成し、親クラスを継承します。
x_epとy_epを定義、それ以外は引き継ぎます。
import random
import math
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0 , x_ep = 1, y_ep = 0):
super().__init__(n_len, x_lim, y_lim, x_posi, y_posi, theta) #x_ep、y_ep以外は親クラスのまま super()で呼び出し
self.x_ep = x_ep #x末端座標定義
self.y_ep = y_ep #y末端座標定義ここでsuper()は親クラスを呼び出す関数です。
複雑なことはやっていませんが、継承するうえで重要になる記載方法で!!
次に行きましょう。
改変ポイント②:throw関数でθを変えずにx_epを決める。y_epとθを計算する。
針を投げる関数です。
針先端のx_posiとy_posiは親クラスの関数と同じで良いです。
つづいて、針末端座標、x_epをランダムで選び、y_epを計算します。
まずはここまでやりましょう。考え方は先に記載した通りです。
import random
import math
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
~~~~~略~~~~~
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
続いてθを求めます。
実は、super().throw()を先に実行していますので、いったんランダムで選ばれています。
この後の処理で上書きすることとします。
まず、cosθを求めます。
「斜辺=針の長さl」と「底辺=針のx座標の末端と先端の差」から計算できます。
次にcosθからθを求めます。θ = arccos(cosθ)で求まります
これを計算すると、0~180°が計算されます。
180°以上の場合を考えましょう。
すでに定義した「y_ep_pm」で「ー」になる場合、θは180°以上になります。(図参照)
この場合、θは360ー(いったん計算したθ)で計算できます。
ここまでを踏まえて、プログラムを書いてみましょう。
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
cos_theta = x_ep_len/self.n_len # cosθ = x座標距離 / 針長さl
theta_dg = math.degrees(math.acos(cos_theta)) #cosθ > θ(ラジアン) > θ(degree)
self.theta = y_ep_pm * theta_dg # 180°以上ならy_ep_pmは-1
if self.theta < 0:
self.theta +=360 #180°以上なら、-theta+360
次に行きましょう。
改変ポイント③:endpoint関数でx_ep、y_epを計算しない
ここは、計算「しない」なので簡単です。サクッと行きましょう。
import random
import math
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
~~~~~略~~~~~
def endpoint(self, xy = 'y'):
x_ep = self.x_ep #x_epはthrowで計算済み
y_ep = self.y_ep #y_epはthrowで計算済み
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'改変ポイント④:y_change関数をここまでの改変に合わせて調整する
y_change関数は前回記事参照。
y_2は親クラスと同様に計算します。y_2_epはもともとθから計算していました。
今回は角度から位置を算出するのは排除したいので、いままで決めた位置座標から計算します。
import random
import math
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
~~~~~略~~~~~
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のyできました。
一旦、ここまでのものを合算して、いろいろprintしてみます。
import random
import math
~~~~~略~~~~~
class Needle:
~~~~~略~~~~~
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0 , x_ep = 1, y_ep = 0):
super().__init__(n_len, x_lim, y_lim, x_posi, y_posi, theta) #x_ep、y_ep以外は親クラスのまま super()で呼び出し
self.x_ep = x_ep #x末端座標定義
self.y_ep = y_ep #y末端座標定義
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
cos_theta = x_ep_len/self.n_len # cosθ = x座標距離 / 針長さl
theta_dg = math.degrees(math.acos(cos_theta)) #cosθ > θ(ラジアン) > θ(degree)
self.theta = y_ep_pm * theta_dg # 180°以上ならy_ep_pmは-1
if self.theta < 0:
self.theta +=360 #180°以上なら、-theta+360
def endpoint(self, xy = 'y'):
x_ep = self.x_ep #x_epはthrowで計算済み
y_ep = self.y_ep #y_epはthrowで計算済み
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
needle = Needle_not_theta(n_len=2, x_lim = 12, y_lim = 12,)
needle.throw() #針を投げて、x、y、x_ep, y_ep, θを再設定
print(f'投げ後x {needle.x_posi}')
print(f'投げ後y {needle.y_posi}')
print(f'投げ後θ {needle.theta}')
print('投げ後x末端', needle.endpoint('x'))
print('投げ後y末端',needle.endpoint('y'))
#三平方の定理から針の長さを計算 math.sqrt()で平方根を計算
hd_len_2jyou = (needle.x_posi - needle.endpoint('x'))**2 + (needle.y_posi - needle.endpoint('y'))**2
print(f'計算針長 {math.sqrt(hd_len_2jyou)}')
print('変換y先端', needle.y_change(3))
print('変換y末端',needle.y_change(1, ep = 'ep'))
hd_len_2jyou = (needle.x_posi - needle.endpoint('x'))**2 + (needle.y_posi - needle.endpoint('y'))**2
print(f'計算針長 {math.sqrt(hd_len_2jyou)}')結果はこうなりました。
投げ後x 6.693850036916482
投げ後y 5.703015188140151
投げ後θ 286.16977791361944
投げ後x末端 7.250819109759437
投げ後y末端 3.7821337623627924
計算針長 2.0
変換y先端 2.703015188140151
変換y末端 -1.2178662376372076
計算針長 2.0うまくできてそうです。
5.プログラムを書いていこう③ ~実行していこう~
すべてをまとめて実行してみましょう。
前回と変えているのは、
・子class「needle_not_theta」の追加
・buffon_main関数のneedle = Needle_not_theta
です。
まずはプログラムはこうなりました!!
import random
import math
class Input_para:
def __init__(self, t_val = 0, l_val= 0, n_val =0):
self.t_val = t_val #間隔:t
self.l_val = l_val #針の長さ:l
self.n_val = n_val #試行回数:n
def inp_val(self, p_type = '', val_type = float): #P_type:t, l, n val_type:float, int
while True:
para_str = input(f'{p_type}を入力:')
try:
para_tc = val_type(para_str) #floatかintに変換
return para_tc #floatかintで返す
except ValueError: #誤った値が入力された場合
print ('数字を入力してください')
else:
break
class Needle:
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0):
self.n_len = n_len #針の長さ n
self.x_lim = x_lim #x最大値
self.y_lim = y_lim #y最大値
self.x_posi = x_posi #針先位置 x
self.y_posi = y_posi #針先位置 y
self.theta = theta #針角度θ
def throw(self):
self.x_posi = random.uniform(0, self.x_lim) #x位置を0~xlimまでの小数に変える
self.y_posi = random.uniform(0, self.y_lim) #y位置を0~ylimまでの小数に変える
self.theta = random.uniform(0, 360) #θを0~360までの小数に変える
def endpoint(self, xy = 'y'): #針先終点計算、xyはどちらを出力するか?
#θをラジアンに変換、cos(ラジアン)、sin(ラジアン)
#x終点 = x + l cos(θ)、y終点 = y + l sin(θ)
x_ep = self.x_posi + self.n_len * math.cos(math.radians(self.theta))
y_ep = self.y_posi + self.n_len * math.sin(math.radians(self.theta))
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = self.y_posi #y_2にy_posi代入
while True:
if y_2 <= t_val: #y_2が間隔t以下
break
else: #y_2が間隔tより大きい
y_2 -= t_val #y_2から tを引く
y_2_ep = y_2 + self.n_len * math.sin(math.radians(self.theta))
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
class Needle_not_theta(Needle): #クラスNeedle_not_theta クラスNeedleを継承
def __init__(self, n_len=1, x_lim = 1, y_lim = 1, x_posi = 0, y_posi = 0, theta =0 , x_ep = 1, y_ep = 0):
super().__init__(n_len, x_lim, y_lim, x_posi, y_posi, theta) #x_ep、y_ep以外は親クラスのまま super()で呼び出し
self.x_ep = x_ep #x末端座標定義
self.y_ep = y_ep #y末端座標定義
def throw(self):
super().throw() #x_posi,y_posi, thetaをランダムで選択
x_ep_len = random.uniform(-self.n_len, self.n_len) # x_posiとx末端座標までの差 -lからlの間で選択
self.x_ep = self.x_posi + x_ep_len # 末端座標までの差 -lからlの間で選択
y_ep_len = math.sqrt((self.n_len**2) - (x_ep_len**2)) # y_posiとy末端座標までの差 三平方の定理
y_ep_pm = random.choice([-1, 1]) # y末端座標計算に使用 +1か-1を選択
self.y_ep = self.y_posi + (y_ep_pm * y_ep_len) # y末端座標 = y先端 + y_ep_len離 or y先端 - y_ep_len
cos_theta = x_ep_len/self.n_len # cosθ = x座標距離 / 針長さl
theta_dg = math.degrees(math.acos(cos_theta)) #cosθ > θ(ラジアン) > θ(degree)
self.theta = y_ep_pm * theta_dg # 180°以上ならy_ep_pmは-1
if self.theta < 0:
self.theta +=360 #180°以上なら、-theta+360
def endpoint(self, xy = 'y'):
x_ep = self.x_ep #x_epはthrowで計算済み
y_ep = self.y_ep #y_epはthrowで計算済み
if xy == 'x':
return x_ep
elif xy == 'y':
return y_ep
else:
return 'error'
def y_change(self, t_val, ep = ''):
y_2 = super().y_change(t_val, ep = '') #y_2はneedleクラスと同じ計算
y_2_ep = self.y_ep - (self.y_posi - y_2) #y_2_ep = y_ep - (y_posi - y_2)
if ep == 'ep':
return y_2_ep #y変更後の終点
else:
return y_2 #y変更後のy
def buffon_main(t_val, l_val, n_val):
num = 0 #試行回数の設定
hit = 0 #あたり回数の設定
limit = 3*t_val #xとyの最大値は 3t
while num < n_val: #試行回数 < 目標試行回数
needle = Needle_not_theta(n_len = l_val, x_lim = limit, y_lim = limit) #針の設定
needle.throw() #針を投げる = x, y, θの再設定
if needle.theta <= 180: #θ <= 180
if needle.y_change(t_val, 'ep') >= t_val:
hit += 1 #交差カウント +1
else:
pass
else: #θ > 180
if needle.y_change(t_val, 'ep') <= 0:
hit += 1 #交差カウント +1
else:
pass
y_2 = needle.y_change(t_val, 'ep')
#print(f'x:{needle.x_posi}, y:{needle.y_posi}, θ:{needle.theta}, y_2_ep:{y_2}')
num += 1 #
print(f'試行回数:{num}')
print(f'交差本数:{hit}')
prob = hit/num #交差する確率
print(f'交差する確率 P = 2l/t(pi) = {prob}')
pi = 2*l_val/(t_val*prob) #pi = 2*l/(t*prob)
print(f'円周率 : {pi}')
para = Input_para()
para.t_val = para.inp_val('間隔 t ', float)
para.l_val = para.inp_val('針の長さ l ', float)
para.n_val = para.inp_val('試行回数 n ', int)
print(f'間隔 t :{para.t_val}, 針の長さ l : {para.l_val}, 試行回数 n : {para.n_val}')
buffon_main(para.t_val, para.l_val, para.n_val)
今回、継承したクラス以外の追加以外何もしていません。
これが「オブジェクト指向」と「継承」の威力です。
では実行してみましょう。前回同様t=4、l=3としてnを変えていってみましょう。
n =10、円周率2.14。まだまだ。
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:10
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10
試行回数:10
交差本数:7
交差する確率 P = 2l/t(pi) = 0.7
円周率 : 2.142857142857143
n = 1000、円周率2.61。まだかな?
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:1000
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 1000
試行回数:1000
交差本数:573
交差する確率 P = 2l/t(pi) = 0.573
円周率 : 2.617801047120419n = 10000、円周率2.53。前回はこのくらいから大体計算できたのですが、、、雲行き怪しい。
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:10000
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000
試行回数:10000
交差本数:5909
交差する確率 P = 2l/t(pi) = 0.5909
円周率 : 2.538500592316805n = 10000000、円周率2.54 ヤバい!!
間隔 t を入力:4
針の長さ l を入力:3
試行回数 n を入力:10000000
間隔 t :4.0, 針の長さ l : 3.0, 試行回数 n : 10000000
試行回数:10000000
交差本数:5891269
交差する確率 P = 2l/t(pi) = 0.5891269
円周率 : 2.5461407380990413なにかミスったようです。
改めて、いろいろと見直して検証しましたが、プログラム自体には問題ありませんでした。
初めに計画した作戦どおりには動かせています。
ということは、そもそも作戦に誤りがあったようですね。
次回は、何がダメだったのかを検証していきます。
To Be Continued : ビュフォンの針を落とす ep3
PyQさんで勉強中!




コメント