
やりつくされたモンティホール問題をあえてやる。
誇張しすぎたモンティホール。
モンティホールの問題はご存じでしょうか
「直感で正しいと思える解答と、論理的に正しい解答が異なる問題」として、過去に大論争を巻き起こした問題です。
これまで多くの方が、いろいろな角度から検証されてきて、答えはもうはっきりしています。でも、くじ引きの問題をやった時から、これもやろうと思ってました。
どうせやるならいろいろと遊んでやろうと思います。
まあ、でも今回はまず順当にやります。
(2021年3月12日:学習開始22日目、PyQさんで勉強中!)
モンティホールの問題は、3つのドアから1つを選びます。
ここは、The doorsですね。いうまでもない超名盤「The doors」の「Light My Fire(ハートに火をつけて)」を聞きながら考えていきます。(曲名から公式YouTubeに飛びます。)
1.モンティホールの問題
今回取り上げる「モンティホールの問題」についてみていきましょう。
といってもWikipediaのモンティ・ホール問題にかなり詳しく記載があり、内容から検証まで説明されています。
ですので、ここでは概要の振り返りにとどめておきます。
まず、「モンティホールの問題のルール」から見てみます。
ルールは以下のとおりです。
①:プレイヤーの前に3つのドアがある。
②:ドアに後ろには、1つは自動車(あたり)、2つはヤギ(はずれ)が置かれている。
③:プレイヤーは3つのうち1つのドアを選ぶ。
④:司会のモンティ・ホール(人名かよ)が残りのドアのうち、ヤギ(はずれ)の一つを開く。
⑤:プレイヤーは「最初に選んだドア」か「モンティが開けなかったドア」を選びなおせる。
⑥:すべてのドアを開く。最終的に選んだドアに自動車(あたり)があればもらえる。
はずれがヤギっていうセンスよ。鳴き声とかで分かるやろ!
まあ、それはいいとして、こんな感じの企画を過去にアメリカのテレビでやってて、⑤のところでプレイヤーはドアを変えるべきか?ということが議論になりました。
正解は、「ドアを変えた方が2倍の確率であたる」です。
これがあまりに直観とズレた答えだったので、当時は数学者でも意見が割れたりしたそうです。
どう思います?確かに違和感ありますよね?だって、始めに選んだドアと変えたドアはもともと同じ確率であたりだったはずなのに、途中のモンティの行動で確率が変わるってマジ?って思いますよね。
この問題の解法は、「確率の計算」や「全パターン実際に書いてみる」といったやり方があり、確かに変えた方が2倍の確率で当たります。
で、今回は、プログラムで実際に試行回数を増やしてやってみて、確率を出してみたいと思います。
2.作戦会議とフローチャート
大まかにやりたいことは、モンティホールの問題を100回、1000回とトライさせて、そのうちあたりが出た回数から確率を計算するということです。
本来のルールならば、モンティが1つドアを開けた後に、プレイヤーがドアを変えるかどうか決めるというものです。
多分、テレビ番組的には、「ドアを変えますか?ファイナルアンサー?」的な心理戦があったはずですが、プログラムに心理戦は扱えません。
今回は、先に「ドアを変更する」or「ドアを変更しない」を先に決めて同じ条件で繰り返しトライするということで進めます。
ここまでをフローチャートに反映さえて書いてみました。
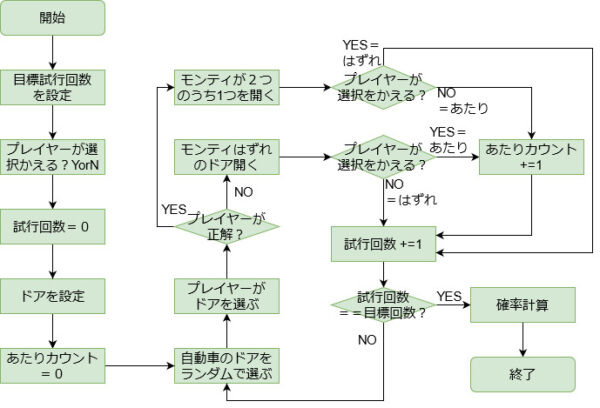
思っていたより複雑になりました。
書いてみて分かったのは、「ドアを変更するかどうか」を先に選択していた場合、最初にドアを選んだ瞬間に「あたり」か「はずれ」が決定している、ということです。よく考えれば当たり前ですが。
しかし、これが「直観と実際の結果がズレる」原因かもしれません。(違うかも・・・)
さて、プログラムを書いていきましょう。
3.プログラムを書いていこう
上から順にみていきましょう。
今回も、学習のためにdefで関数を定義しながら書いていきます。
また、あきらかにrandomは使用するので、冒頭でインポートしておきます。
まずは、「目標試行回数の設定」と「プレイヤーの選択を決定」です。
import random
def sim_choice():
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
plyer_choice = input('ドアを変更しますか? YES = y or NO = n :') #ドア変更するか?
if plyer_choice == 'y': #ドア変更あり
print(f'試行回数:{num_sim}回、ドア変更あり')
elif plyer_choice == 'n': #ドア変更なし
print(f'試行回数:{num_sim}回、ドア変更なし')
return [num_sim, plyer_choice] #リストで返す[試行回数, ドア変y or n]
sim_choce()いくつかポイントがあります。
まず、「inputは文字列が入力される」ということです。そのため、num_simはint()で整数に置き換えています。
次に、入力した内容をprintすることにしました。これで自分が何を入れたかを見れます。
最後に、returnでは[整数(試行回数), ‘y’か’n'(ドアを変えるかどうか)]を返すことにしました。
実行してみましょう。
試行回数を入力してください:10
ドアを変更しますか? y or n :y
試行回数:10回、ドア変更ありここでは、試行回数に10を、ドア変更の有無にy(yes)を入力しました。うまく動作しています。
これは、試行回数には数字を、ドアの変更にはyかnを入れたので正しく動きました。
では、試行回数にローマ字「j」を入れるとどうなるでしょうか?
試行回数を入力してください:j
Traceback (most recent call last):
File "monty.py", line 12, in <module>
sim_choce()
File "monty.py", line 4, in sim_choce
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
ValueError: invalid literal for int() with base 10: 'j'当然、ローマ字はintで整数にできないので、エラーがでました。
これまで、エラーから逃げるための処理として、whileでループさせておいてif / elif /elseを使ってきました。
たとえば過去の記事「pV=nRT 単位換算地獄 ~気体の状態方程式をPythonで! ep 1~」では、
if 正しい入力1:→処理開始、ループ終了
elif 正しい入力2: → 処理開始、ループ終了
else:(=誤った入力) → 正しい値での入力を促してループを戻る
という感じの処理をしています。
今回は、別のやり方として、try / except / else/ finallyを学んだのでこれでやってみます。
まず、エラーのパターンを考えます。さっきやったのは、試行回数に文字列(str)を入れたというものでした。ほかのパターンも考えてみましょう。
エラーパターン①:試行回数に文字列(str) (さっきのやつ)
エラーパターン②:試行回数に小数(float)
エラーパターン③:ドアを変更するか?にy、n以外の文字列(str)
エラーパターン④:ドアを変更するか?に整数(int)
エラーパターン⑤:ドアを変更するか?に小数(float)
面倒ですが、それぞれやってみましょう。①はもうみたので飛ばします。
あと、必要なのは、エラーの最後の行だけですので、ほかは割愛します。
エラーパターン②:試行回数に小数(float)
ValueError: invalid literal for int() with base 10: '10.5'エラーパターン①、②ともにエラー名はValueErrorでした。
エラーパターン③:ドアを変更するか?にy、n以外の文字列(str)
エラーパターン④:ドアを変更するか?に整数(int)
エラーパターン⑤:ドアを変更するか?に小数(float)
実はこれらは、現時点でエラーは出ません。yかn以外でもプログラムは先に進みます。
この処理はちょっと後回しにして、試行回数のエラーを処理しましょう。
プログラムを書く時のポイントは以下です。
・きちんとした値が入るまで、ループさせたいので、while Trueでループさせます。
・エラーの起こしそうな処理をtryで囲い込む。
・エラーを起こした場合の処理をexcept (エラー名):の下にインデントして書く
・問題なければ(= else:)、breakでループから抜ける。
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
plyer_choice = input('ドアを変更しますか? YES = y or NO = n :') #ドア変更するか?
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
break
if plyer_choice == 'y': #ドア変更あり
print(f'試行回数:{num_sim}回、ドア変更あり')
elif plyer_choice == 'n': #ドア変更なし
print(f'試行回数:{num_sim}回、ドア変更なし')
return [num_sim, plyer_choice] #リストで返す[試行回数, ドア変y or n]
sim_choce()このようになりました。ここでは書きませんが、動かしてみると正しく動作しました。
では、次に進みましょう。
「試行回数=0」「ドアを設定」「あたりカウント=0」まではいっきに行きます。
ここから先は、モンティホールのゲームの一連の流れになりますので、まとめて一つの関数にした方がよさそうです。
また、先ほど作った関数sim_choce()を、これからつくる関数に反映させたいと思います。sim_choce()では、「目標試行回数」と「ドアの選択」が出力されていました。ですのでこれから作る関数はこの2変数を受け取れる関数にすればよさそうです。
def monty(num, y_or_n):
sim_count = 0 #これまでの試行回数
door = [1,2,3] #ドアは3つ。番号を付けた。
car_count = 0 #あたりの回数(あたりは自動車)こうなりました。montyの関数は2変数numとy_or_nをインプットできます。
ドアには番号を振りました。この番号とあたり、はずれ、プレイヤーの選択を割り当てていきます。
次に行きましょう。
「自動車のドアをランダムで選ぶ」「プレイヤーのドアを選ぶ(ここもランダム)」まで行きましょう。フローチャートではここまで戻ってきている矢印がありますが、今は無視して進めます。
def monty(num, y_or_n):
~~~略~~~
car = random.choice(door) #あたりのドアをランダムで
player = random.choice(door) #プレイヤーが選ぶドアををランダムでこれでOKです。ちなみにrandomは最初にimportしています。次に行きましょう。
ここから分岐です。「プレイヤーが正解しているかどうか?」でまず分岐します。
そこから先は一見ややこしいですが、実際はひとつずつ分岐させていけばよいので、簡単そうです。
フローチャートの「試行回数+=1」まで進みましょう。
def monty(num, y_or_n):
~~~略~~~
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if y_or_n == 'y':
pass #不正解の場合、pass
elif y_or_n == 'n':
car_count += 1 #正解の場合、あたりカウント+1
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if y_or_n == 'y': #正解の場合、あたりカウント+1
car_count += 1 #正解の場合、あたりカウント+1
elif y_or_n == 'n':
pass #不正解の場合、pass
sim_count += 1ここまで行きました。
door = [1, 2. 3]からモンティがはずれ(ヤギ)のドアを選択できるように、removeで取り除いていっています。ですので、ここまで来た時点でdoorは数字が抜けた状態になっています。
しかし、苦労してモンティが選択できるドアを絞っていってますが、monty_choice(=モンティの開けるドア)は結果になにも影響していないことが分かります。
さて、いったんここまでの出来具合を確かめたいので、「1回試行するプログラム」として動かしてみたいと思います。いままで作ったのに、いくつかコードを加えて以下のようにしました。
import random
def sim_choce():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
plyer_choice = input('ドアを変更しますか? YES = y or NO = n :') #ドア変更するか?
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
break
if plyer_choice == 'y': #ドア変更あり
print(f'試行回数:{num_sim}回、ドア変更あり')
elif plyer_choice == 'n': #ドア変更なし
print(f'試行回数:{num_sim}回、ドア変更なし')
return [num_sim, plyer_choice] #リストで返す[試行回数, ドア変y or n]
def monty(num, y_or_n):
sim_count = 0 #これまでの試行回数
door = [1, 2, 3] #ドアは3つ。番号を付けた。
car_count = 0 #あたりの回数(あたりは自動車)
car = random.choice(door) #あたりのドアをランダムで
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if y_or_n == 'y':
pass #不正解の場合、pass
elif y_or_n == 'n':
car_count += 1 #正解の場合、あたりカウント+1
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) ##montyはヤギのドアから選ぶ
if y_or_n == 'y': #正解の場合、あたりカウント+1
car_count += 1 #正解の場合、あたりカウント+1
elif y_or_n == 'n':
pass #不正解の場合、pass
sim_count += 1
print(f'試行回数{sim_count}、あたり回数{car_count}')
print(f'自動車のドア{car}、最初の選択{player}、モンティの選択{monty_choice}')
sim = sim_choce()
monty(sim[0],sim[1])動かしてみましょう。3回動かしてみました。
試行回数を入力してください:1
ドアを変更しますか? YES = y or NO = n :y
試行回数:1回、ドア変更あり
試行回数1、あたり回数1
自動車のドア2、最初の選択1、モンティの選択3
試行回数を入力してください:100
ドアを変更しますか? YES = y or NO = n :n
試行回数:100回、ドア変更なし
試行回数1、あたり回数0
自動車のドア1、最初の選択3、モンティの選択2
試行回数を入力してください:1
ドアを変更しますか? YES = y or NO = n :10
試行回数1、あたり回数0
自動車のドア1、最初の選択2、モンティの選択3最初にインプットする試行回数は今は使えていないので、1でも100でも動作は同じです。
きちんと実際の試行回数は1、あたり回数は当たれば1、外れれば0になっています。
一方で、ドア変更の有無については修正が必要です。yかnを入れた場合は正しく動いていますが、数字を入れた場合は、無条件ではずれになっています。
ドア変更の選択は、「エラー」として認識されないので、try / exceptでは補足できないようです。
先に進む前に、sim_choiceの方を修正しておきます。
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
plyer_choice = input('ドアを変更しますか? YES = y or NO = n :') #ドア変更するか?
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
pass
if plyer_choice == 'y': #ドア変更あり
print(f'試行回数:{num_sim}回、ドア変更あり')
break
elif plyer_choice == 'n': #ドア変更なし
print(f'試行回数:{num_sim}回、ドア変更なし')
break
else:
print('ドアを変更はyかnを入れてください')
return [num_sim, plyer_choice] #リストで返す[試行回数, ドア変y or n]これで、ドア選択でyかn以外を入れると戻るようになりました。
ここから、試行回数による分岐になります。
ここも、細かく書くとややこしいので、いっきに行きたいと思います。
追加と修正のポイントは3つです。
①:sim_count(実際の試行回数)== num(目標試行回数)となるまで繰り返す。
②:door設置の位置を変える。(doorのリストから数字が抜かれているので毎回初期化する)
③:あたり確率=あたり回数/試行回数
これに加えて、出力する内容に合わせてちょっといじって完成です。
import random
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
plyer_choice = input('ドアを変更しますか? YES = y or NO = n :') #ドア変更するか?
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
pass
if plyer_choice == 'y': #ドア変更あり
print(f'試行回数:{num_sim}回、ドア変更あり')
break
elif plyer_choice == 'n': #ドア変更なし
print(f'試行回数:{num_sim}回、ドア変更なし')
break
else:
print('ドアを変更はyかnを入れてください')
return [num_sim, plyer_choice] #リストで返す[試行回数, ドア変y or n]
def monty(num, y_or_n):
sim_count = 0 #これまでの試行回数
car_count = 0 #あたりの回数(あたりは自動車)
while True:
if sim_count != num:
door = [1, 2, 3] #ドアは3つ。番号を付けた。
car = random.choice(door) #あたりのドアをランダムで
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if y_or_n == 'y':
hantei = 'はずれ' #不正解の場合
elif y_or_n == 'n':
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if y_or_n == 'y': #正解の場合、あたりカウント+1
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
elif y_or_n == 'n':
hantei = 'はずれ' #不正解の場合
sim_count += 1
print(f'試行No{sim_count}、{hantei}')
else:
car_prob = 100*car_count/sim_count #あたった確率%
print(f'試行回数{sim_count}、あたり回数{car_count}、あたり確率{car_prob:3f}%')
break
sim = sim_choice()
monty(sim[0],sim[1])動かしてみましょう。試行回数は10、扉の変更ありとしました。
試行回数を入力してください:10
ドアを変更しますか? YES = y or NO = n :y
試行回数:10回、ドア変更あり
試行No1、はずれ
試行No2、あたり
試行No3、はずれ
試行No4、はずれ
試行No5、あたり
試行No6、はずれ
試行No7、あたり
試行No8、あたり
試行No9、あたり
試行No10、あたり
試行回数10、あたり回数6、あたり確率60.000000%うまくできましたね。では、もっと試行回数を増やしてみましょう。
毎回あたり、はずれを出すと行数が膨大になるので、printしないようにして、最終の結果だけ出るようにします。
試行回数は10000回、ドアの変更ありとなしでやってみました。
試行回数を入力してください:10000
ドアを変更しますか? YES = y or NO = n :y
試行回数:10000回、ドア変更あり
試行回数10000、あたり回数6627、あたり確率66.270000%試行回数を入力してください:10000
ドアを変更しますか? YES = y or NO = n :n
試行回数:10000回、ドア変更なし
試行回数10000、あたり回数3286、あたり確率32.860000%お~~~!
確かに「ドア変更あり」と「ドア変更なし」の確率はそれぞれ大体2/3と1/3になりました。
Q.E.D.
と、ここで終わっても良いのですが、最初にドア変更を自分で決めるのが面倒に感じます。
ドアを選択するところで分岐して、変更した場合と変更しなかった場合を同時に走らせることが出来そうです。
要は、いずれの試行も「変更していたらあたり」か「変更していなかったらあたり」のどちらかに分類されるはずです。
修正する点は7点。
①:dif sim_choice()から「ドアの変更」に関するパートをバッサリカットする。
②:def monty(num)と変数を試行回数のみにする。
③:def montyの中に「ドアを変えた場合のあたり回数」と「変えない場合のあたり回数」をカウント
④:def montyでドアの変更に関するパートをバッサリカット
⑤:初めの選択プレイヤーが正解→変えない場合のあたり回数+=1
⑥:初めの選択プレイヤーが不正解→変えた場合のあたり回数+=1
⑦:確率の計算、printをこれら変更に合わせて修正。
するとこうなりました。
import random
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
print(f'試行回数:{num_sim}回')
break
return num_sim #数字で返す
def monty(num):
sim_count = 0 #これまでの試行回数
change_car = 0 #ドアを変えた場合のあたりの回数(あたりは自動車)
not_change_car = 0 #ドアを変えない場合のあたりの回数(あたりは自動車)
while True:
if sim_count != num:
door = [1, 2, 3] #ドアは3つ。番号を付けた。
car = random.choice(door) #あたりのドアをランダムで
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
not_change_car += 1 #正解の場合、あたりカウント+1
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
change_car += 1 #正解の場合、あたりカウント+1
sim_count += 1
#print(f'試行No{sim_count}、{hantei}')
else:
change_car_prob = 100*change_car/sim_count #あたった確率%
print(f'試行回数{sim_count}、ドアを変更した場合のあたり回数{change_car}、あたり確率{change_car_prob:3f}%')
not_change_car_prob = 100*not_change_car/sim_count #あたった確率%
print(f'試行回数{sim_count}、ドアを変更しない場合のあたり回数{not_change_car}、あたり確率{not_change_car_prob:3f}%')
break
sim = sim_choice()
monty(sim)実際は、もっと削れますが元のを生かしてこれでよいでしょう。結果はこうなりました。
試行回数を入力してください:100000
試行回数:100000回
試行回数100000、ドアを変更した場合のあたり回数66970、あたり確率66.970000%
試行回数100000、ドアを変更しない場合のあたり回数33030、あたり確率33.030000%10万回の計算ですが、一瞬で完了しました。
やはり、ドアを変えた方が倍の確率であたることが分かります。まあ、そうなりますよね。
面白いのは、始める前は違和感のあったこの結果ですが、プログラムを追いかけていくとこの結果になって当然と思えるようになります。今回はここまでにします。
次回は、つくったプログラムでもう少し遊びます。(やることあるのか?)
To Be Continued : モンティホール・アウトレイジ ep 2
PyQさんで勉強中!





コメント