
ここまできたらとことんやってやろう。
もはや別物だ!
記事①:モンティ・ホール問題をPythonで検証する ~モンティホール・アウトレイジ ep 1~
記事②:モンティ・ホールの問題を100個のドアで説明するの納得いかない~モンティホール・アウトレイジ ep 2~
前回は、モンティホールの問題の初期条件をいじって、遊びました。ただ、結果は予想通りという感じもありました。
今回はさらに条件を変えて複雑にすることで、予想ができないところまで持っていきたいと思います。想像を絶する答えが出てきたらうれしいですが、どうなることでしょうか?
(2021年3月18日:学習開始27日目、PyQさんで勉強中!)
ここから更なるカオスに突入していきます。カオスより愛をこめて。
レッチリとは少し違う方向のミクスチャーロックのオリジネーター「311」の「From Chaos」より「Amber」を聞きながら行きましょう。
(曲名から公式YouTubeに飛びます。夏に聞きたい曲。ロック、ラップからハワイアンまでごった煮(=ミクスチャー)です。)
よーし、やっていこう!。
意図はしていませんでしたが、衝撃の結果でした。
また、これも意図していませんでしたが、「確率の重みづけ」や「リストを文字列に変換する方法」も途中(4.5)でやっています。
1.ここまでの振り返り
モンティホールの問題のルールはこんな感じです。
①:プレイヤーの前に3つのドアがある。
②:ドアに後ろには、1つは自動車(あたり)、2つはヤギ(はずれ)が置かれている。
③:プレイヤーは3つのうち1つのドアを選ぶ。
④:司会のモンティ・ホール(人名かよ)が残りのドアのうち、ヤギ(はずれ)の一つを開く。
⑤:プレイヤーは「最初に選んだドア」か「モンティが開けなかったドア」を選びなおせる。
⑥:すべてのドアを開く。最終的に選んだドアに自動車(あたり)があればもらえる。
まず初めに、順当にルールに従ってプログラムを組みました。モンティホール・アウトレイジ ep 1
次は、
「なにも考えないヤツを出す」
「ドアの数を増やす」
「ドアの数をめちゃめちゃ増やす」
ってことをやりました。モンティホール・アウトレイジ ep 2
ドアを増やすってことは、最初のルールから逸脱していっているって事ですよね?
という事で今回は、
「あえて前提のルールを逸脱して何か面白くならないか?」
っていう視点でやっていきます。
2.ルールを破ろう!
あらためてルールを見直して、(ドア数以外の)前提となっていることを考えてみました。
前提①:最初に決まった「あたり」と「はずれ」は動かない
前提②:モンティはどれがあたりかを知っている
前提③:最初に「あたり」と「はずれ」が均一にドアに割り振られる
という事かなと思います。1つずつ見ていきましょう。
前提①:最初に決まった「あたり」と「はずれ」は動かない
これを崩すと、どうなうでしょうか?
モンティがドアを開けて「はずれ」を見せたあと、再度シャッフルされるという事になります。
この時点で2つのドアが残り、50:50であたりになるわけですね。
ということは、どちらのドアを選んでも等確率。モンティの動作に選択肢の排除以外の意味がなくなります。
これは面白くない。却下!!
前提②:モンティはどれがあたりかを知っている
これを崩す
= モンティがあたりを知らない
= モンティのドア開示であたりを可能性がある
= ゲーム終了。
これも面白くない。却下!!
前提③:最初に「あたり」と「はずれ」が均一にドアに割り振られる
これが崩れると何が起こるでしょうか。最初に「あたり」と「はずれ」が「不均一に」ドアに割り振られるとはどういう事でしょうか?
具体例でみていきましょう。
ドアA、B、Cがあって、3:2:1の確率であたりが割り振られる。
という事になると思います。
この場合、どうすればあたりを選べる確率が最大になるのでしょうか?
ただし、プレイヤーは、確率3,2,1のドアがそれぞれどのドアか分かっているものとします。
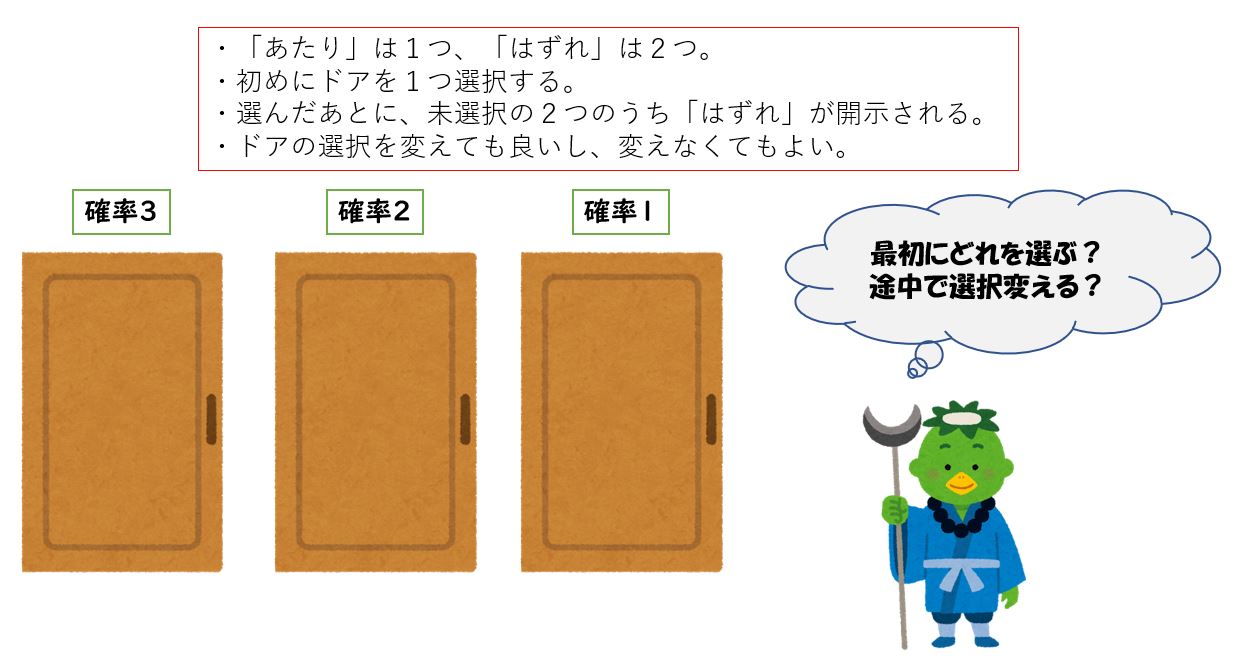
わ、分からない!
最初にAを選んで保持した方がよいのか?Bを選んで変える方がよいのか?むしろCを選んで変える方がよいのか?
直観的に分からない!これは面白い。この方向でいきましょう!!
ということで今回は、
「ドアA、B、Cがあり、それぞれ、3:2:1の確率であたりが入っている。その後モンティーホールのルールでゲームを行ったとき、どのような戦略をすればあたりを選ぶ確率を最大化できるか?」
というのを明らかにしていきます!!
3.作戦会議① ~「ヤツ」再降臨~
今回、最初にあたりを選ぶ確率に「重みづけ」をするという事にしました。
そして、最終的に出したい答えは、
「最初に選ぶドアはどれで、選択肢変更はした方がよいかどうか?」
ということです。
3つのドア X 選択肢変更の有無(2)で計6この戦略が考えられます。
ひとつずつ確かめて確率を出し、大小比較しても当然答えをだせますが、面倒です。
そこで、いろんなパターンを1回で試すことを考えてみましょう。そう「ヤツ」の登場です。
前回やった、「クレイジーなプレイヤー」=何も考えずに選択するヤツです。
こいつは、試行回数の中で、いろんなパターンをランダムに実行していきます。
うまく使えば、端から端までいっきに試してくれるので、工夫すれば全パターンの確率を一発で出せそうです。
前回つくった、このプログラムを軸として改変していきます。
import random
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
print(f'試行回数:{num_sim}回')
break
return num_sim #数字で返す
def monty(num):
sim_count = 0 #これまでの試行回数
car_count = 0 #あたりの回数(あたりは自動車)
y_car_count = 0 #ドアを変えてあたりが出た回数
n_car_count = 0 #ドアを変えずにあたりが出た回数
while True:
if sim_count != num:
door = [1, 2, 3] #ドアは3つ。番号を付けた。
car = random.choice(door) #あたりのドアをランダムで
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
door_change = random.choice(['y', 'n']) #プレイヤーがドアを変えるか?
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if door_change == 'y':
hantei = 'はずれ' #不正解の場合
elif door_change == 'n':
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if door_change == 'y': #正解の場合、あたりカウント+1
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
elif door_change == 'n':
hantei = 'はずれ' #不正解の場合
if hantei == 'あたり' and door_change == 'y':
y_car_count += 1
elif hantei == 'あたり' and door_change == 'n':
n_car_count += 1
sim_count += 1
else:
car_prob = 100*car_count/sim_count #あたった確率%
print(f'試行回数{sim_count}、あたり回数{car_count}、あたり確率{car_prob:3f}%')
print(f'ドアを変えてあたり{y_car_count}回、ドアを変えずにあたり{n_car_count}回')
break
sim = sim_choice()
monty(sim)4.作戦会議② ~確率操作~
もう一つ考える必要があるのが、
「確率の重みづけをどうするか?」
という点です。
まず、パッと思いついたのは、
「数字1,2,3,4,5,6からランダムに選ぶ。1,2,3はドアA、4,5はドアB、6はドアC」というやり方です。
まあ、これでも出来そうです。ただ、過去くじ引きのところ(このへん確率の悪魔 vs Python ep 3)でやったのと大体同じですね。せっかくなんで他の書き方を考えてみます。
そこで思い付いたのが、「正規表現」(reモジュール)を使う手法です。
(最近やったので。。。ちょっと無理やりです。。。勉強のためなので。。。)
正規表現のちゃんとした解説はpythonドキュメントre-正規表現操作やUX MILKさんの「Pythonの正規表現の基本的な使い方」にあるのでご参照ください。
概略でいうと「特定の文字列やパターンを判定する」という事です。具体的にやってみます。
数字のリスト num_list = [1, 2 ,4 ,23 ,24,100 , 600 ,10000] から2ケタの数字23,24を取り出すことを考えてみましょう。
正規表現は非常に多様な表現がありますが、ここでは「2ケタの数字の表現」のみに絞ります。
2ケタの数字とは、「0~9までの数字」が「2つ並んだ」状態です。
(厳密には、10の位が0の場合は2ケタの数字ではないですが、ここではこれも含めます。」
これを表現するためには、以下の記号を使います。
・ 「^」→文字列の先頭
・ 「$」→文字列の最後
・ 「\d」→0~9の数字 (¥はバックスラッシュでも同じです)
・ 「{n}」→前の文字をn回繰り返し
これらを組み合わせると、「2ケタの数字」は「^\d{2}$」と表せます。
次にre.mathch(xxx, yyy)を使います。xxxに正規表現、yyyに判定する対象を入れます。
yyyがxxxの表現に合致していればTrue、合致していなければFalseとなります。
一度、簡単に検証してみましょう。
import re #reモジュール呼び出し
num_list = [1, 2 ,4 ,23 ,24,100 , 600 ,10000]
for num in num_list: #ひとつずつ数字取り出し
if re.match('^\d{2}$', num): #2桁の数字か?
print(num)では出力してみましょう!
Traceback (most recent call last):
File "test.py", line 4, in <module>
if re.match('^\d{2}$', num): #2桁の数字か?
File "C:\ProgramData\Anaconda3\lib\re.py", line 191, in match
return _compile(pattern, flags).match(string)
TypeError: expected string or bytes-like objectあれ、、エラーがでた・・・。
エラーの内容を読むと、どうやら文字列strが求められています。
よく考えると^\d{2}$も「’’」で囲っているので、文字列として扱っています。
ということは数字のままでは正規表現で判定できないようです。
修正して再度やってみましょう。
import re #reモジュール呼び出し
num_list = [1, 2 ,4 ,23 ,24,100 , 600 ,10000]
for num in num_list: #ひとつずつ数字取り出し
st_num = str(num) #数字を文字列に
if re.match('^\d{2}$', st_num): #2桁の数字か?
print(num)で結果はこうです。
23
24無事、2ケタの数字だけが出力されています。
さて、前置きが長くなりましたが、1ケタの数字を3つ、2ケタの数字を2つ、3ケタの数字を1つ用意して、この正規表現で判定すれば、「確率の重みづけ」を表現できますね。
これを利用したいと思います。
4.5 確率操作 random.choises(選択肢, weights)
(追記)
終わったあとに、もっと良いやり方あるんじゃないかと思って調べると、当然ありました。
Pythonのrandom.choices関数を利用してランダム値に重み付けする方法を現役エンジニアが解説【初心者向け】
random.choices(選択肢, weights = 重み)で行けるようです。
choiceではなくchoice「s」です。(ここで30分囚われてしまった、、、)
今回の場合はこんな感じです。(下で検証しますが、間違えています。)
import random #randomモジュール
door = ['A', 'B', 'C'] #ドアの名前
w = [3, 2, 1] #確率の重みづけ
door_choice = random.choices(num_list, weights = w) #数字選択うわ、マジで簡単。print(door_choice)をつけて出力するとこうなります。
['B']おっと、一筋縄ではいかないですね。
choiceではリストの中の1要素を取り出していましたが、choice「s」ではリストつきのままです。
choice「s」は
choices(選択肢, k=数字n, whights =w)
として使用するとn個の要素を取り出すことができるので、リストでかえって来た方が都合がよいということですね。
リストを文字列にするには、どうすればよいのでしょうか?
ありました、HEADBOOSTさんのPythonのリストと文字列を相互に変換する方法まとめ参照
「 ’’.join([リスト]) 」が使えそうです。
こんな感じ。
import random
door = ('A', 'B', 'C') #ドアの名前
w = [3, 2, 1] #確率の重みづけ
door_choice = random.choices(door, weights=w) #数字選択
print(''.join(door_choice))出力するとこうなります。
Bできましたね。本来であれば、リスト内の要素をくっつけるものですが、一文字でも適応できました。
こうなると本当に重みづけできているか心配になってきました。
ちょっと検証しましょう。1000回繰り返して、重みづけできているか見てみます。
import random #randomモジュール
A_count = 0
B_count = 0
C_count = 0
for i in list(range(1000)):
door = ['A', 'B', 'C'] #ドアの名前
w = [3, 2, 1] #確率の重みづけ
door_cho = random.choices(door, weights=w) #数字選択
door_choice = ''.join(door_cho) #一文字リストを文字列に
if door_choice == 'A':
A_count += 1
elif door_choice == 'B':
B_count += 1
else:
C_count +=1
print(f'A : {A_count}回')
print(f'B : {B_count}回')
print(f'C : {C_count}回')結果はこのようになりました。
A : 484回
B : 325回
C : 191回うまくできてそうです。
これは便利ですね。ちょっと罠もありましたが、どこかで使えそうです。
5.コードを書いていこうわ
基本的には、以前のプログラムを使うので、そこから変わるところを考えましょう。
まずは、数字が多くてややこしいので、ドアの名前を1、2、3からA、B、Cに変更しました。
ドアのあたりの確率に重みづけをして、あたりのドアを選びます。
import re #reモジュール
import random #randomモジュール
def door3_choice():
door = ['A', 'B', 'C'] #ドアの名前
num_list = [1, 2, 3, 11, 12, 101] #確率の重みづけ
num_choice = str(random.choice(num_list)) #数字選択
if re.match('^\d{1}$', num_choice):
return 'A'
elif re.match('^\d{2}$', num_choice):
return 'B'
else:
return 'C'これを単独で動かしてみましょう。door3_choice()で何度か実行しました。
分かりやすくするため、reuturn [‘A’, num_choice]のようにして、出力しました。
結果は以下です。
['A', '2']
['B', '12']
['C', '101']うまく行ってそうです。
ここでは、A、B、Cが均等に出ているように見えますが、実際はCはなかなか出ませんでした。
次の変更点です。ゲームの中身(def monty(num):)をいじっていきます。
上で触れたように、ドアの数 x 選択肢ですので、6種類の場合分けが必要になります。
さらに、それぞれの場合で「合計何回発生したか?」と「あたりは何回発生したか?」をカウントする必要があります。
つまり、6通りに対して「合計回数」と「あたり回数」を事前に定義する必要があります。
こんな感じです。
def monty(num):
sim_count = 0 #これまでの試行回数
car_count = 0 #あたりの回数(あたりは自動車)
A_y_tot = 0 #ドア初期選択A、変更あり、以下同じ
A_n_tot = 0
B_y_tot = 0
B_n_tot = 0
C_y_tot = 0
C_n_tot = 0
A_y_car = 0
A_n_car = 0
B_y_car = 0
B_n_car = 0
C_y_car = 0
C_n_car = 0さらに、1回試行ごとにこれら数字のカウントを変更していく必要があります。
if player == 'A' and door_change == 'y':
A_y_tot += 1 #Aかつ変更の回数+1
if hantei == 'あたり':
A_y_car += 1 #Aかつ変更のあたり回数+1
elif player == 'A' and door_change == 'n':
A_n_tot += 1 #Aかつ変更なしの回数+1
if hantei == 'あたり':
~~~~略~~~~
else:
C_n_tot += 1 #Bかつ変更なしの回数+1
if hantei == 'あたり':
C_n_car += 1 #Bかつ変更のあたり回数+1面倒ですが終わりました。
元のプログラムでは、「初めにあたりを選ぶかどうか」で場合分けして、「初めにあたりなら変更なしがあたり」「初めにはずれなら変更ありであたり」と分けています。
この考え方は、あたりの確率の重みづけの変更の影響を受けないので、そのままのプログラムを使えます。
全部くっつけて、場合分けしてprint、その他余分なものを消してこんな感じです。
import random
import re #reモジュール
def sim_choice():
while True:
try:
num_sim = int(input('試行回数を入力してください:')) #試行回数入力、文字列を数字に。
except ValueError: #ValueErrorはnum_simに小数か文字列を入れると発生。
print('試行回数には数字を入れてください。')
else: #正常終了時の処理
print(f'試行回数:{num_sim}回')
break
return num_sim #数字で返す
def door3_choice():
door = ['A', 'B', 'C'] #ドアの名前
num_list = [1, 2, 3, 11, 12, 101] #確率の重みづけ
num_choice = str(random.choice(num_list)) #数字選択
if re.match('^\d{1}$', num_choice):
return 'A'
elif re.match('^\d{2}$', num_choice):
return 'B'
else:
return 'C'
def monty(num):
sim_count = 0 #これまでの試行回数
car_count = 0 #あたりの回数(あたりは自動車)
A_y_tot = 0 #ドア初期選択A、変更あり、以下同じ
A_n_tot = 0
B_y_tot = 0
B_n_tot = 0
C_y_tot = 0
C_n_tot = 0
A_y_car = 0
A_n_car = 0
B_y_car = 0
B_n_car = 0
C_y_car = 0
C_n_car = 0
while True:
if sim_count != num:
door = ['A', 'B', 'C'] #ドアは3つ。A,B,Cを付けた。
car = door3_choice() #あたりのドアをランダムでA,B,Cから選ぶ
player = random.choice(door) #プレイヤーが選ぶドアををランダムで
door_change = random.choice(['y', 'n']) #プレイヤーがドアを変えるか?
if car == player: #初めにプレイヤーが正解
door.remove(car) #ドアから、自動車=プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if door_change == 'y':
hantei = 'はずれ' #不正解の場合
elif door_change == 'n':
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
else: #初めにプレイヤーがはずれ
door.remove(car) #ドアから、自動車のドアを外す。
door.remove(player) #ドアから、プレイヤーのドアを外す。
monty_choice = random.choice(door) #montyはヤギのドアから選ぶ
if door_change == 'y': #正解の場合、あたりカウント+1
car_count += 1 #正解の場合、あたりカウント+1
hantei = 'あたり'
elif door_change == 'n':
hantei = 'はずれ' #不正解の場合
if player == 'A' and door_change == 'y':
A_y_tot += 1 #Aかつ変更の回数+1
if hantei == 'あたり':
A_y_car += 1 #Aかつ変更のあたり回数+1
elif player == 'A' and door_change == 'n':
A_n_tot += 1 #Aかつ変更なしの回数+1
if hantei == 'あたり':
A_n_car += 1 #Aかつ変更のあたり回数+1
elif player == 'B' and door_change == 'y':
B_y_tot += 1 #Bかつ変更の回数+1
if hantei == 'あたり':
B_y_car += 1 #Bかつ変更のあたり回数+1
elif player == 'B' and door_change == 'n':
B_n_tot += 1 #Bかつ変更なしの回数+1
if hantei == 'あたり':
B_n_car += 1 #Bかつ変更のあたり回数+1
elif player == 'C' and door_change == 'y':
C_y_tot += 1 #Cかつ変更の回数+1
if hantei == 'あたり':
C_y_car += 1 #Cかつ変更のあたり回数+1
else:
C_n_tot += 1 #Cかつ変更なしの回数+1
if hantei == 'あたり':
C_n_car += 1 #Cかつ変更のあたり回数+1
sim_count += 1
else:
car_prob = 100*car_count/sim_count #あたった確率%
print(f'試行回数{sim_count}、あたり回数{car_count}、あたり確率{car_prob:3f}%')
print(f'ドア選択A ドア変更あり トータル{A_y_tot}回、あたり{A_y_car}回、あたり確率{100*A_y_car/A_y_tot:.3f}%')
print(f'ドア選択A ドア変更なし トータル{A_n_tot}回、あたり{A_n_car}回、あたり確率{100*A_n_car/A_n_tot:.3f}%')
print(f'ドア選択B ドア変更あり トータル{B_y_tot}回、あたり{B_y_car}回、あたり確率{100*B_y_car/B_y_tot:.3f}%')
print(f'ドア選択B ドア変更なし トータル{B_n_tot}回、あたり{B_n_car}回、あたり確率{100*B_n_car/B_n_tot:.3f}%')
print(f'ドア選択C ドア変更あり トータル{C_y_tot}回、あたり{C_y_car}回、あたり確率{100*C_y_car/C_y_tot:.3f}%')
print(f'ドア選択C ドア変更なし トータル{C_n_tot}回、あたり{C_n_car}回、あたり確率{100*C_n_car/C_n_tot:.3f}%')
break
sim = sim_choice()
monty(sim)いやいや、長い長い。
たぶん、もっとうまい書き方があると思いますが、まあ仕方ないですね。
では実行してみました。試行回数は100000回(10万回)です。
試行回数を入力してください:100000
試行回数:100000回
試行回数100000、あたり回数50212、あたり確率50.212000%
ドア選択A ドア変更あり トータル16798回、あたり8436回、あたり確率50.220%
ドア選択A ドア変更なし トータル16620回、あたり8318回、あたり確率50.048%
ドア選択B ドア変更あり トータル16660回、あたり11152回、あたり確率66.939%
ドア選択B ドア変更なし トータル16584回、あたり5507回、あたり確率33.207%
ドア選択C ドア変更あり トータル16597回、あたり13891回、あたり確率83.696%
ドア選択C ドア変更なし トータル16741回、あたり2908回、あたり確率17.371%えーーーーーーーーマジかーーーーーーー!
これは驚きました。正解は「最初にドアCを選び、変更あり」でした。
しかも83%という高確率で。
どこか間違えていないでしょうか?
まず、変更なしだけピックアップしてみます。
ドアAは約50%、ドアBは約33%、ドアCは約17%です。
変更なしであれば、最初のドアのあたり確率3:2:1のままのはずなので、確かにそういう結果が出てきています。
変更ありの方はよく見ると、変更なしの余事象(100-変更なし)になっていることが分かります。
あ、、、、そういえばそうだった。
そもそもモンティ・ホールの問題は、通常のルールでも
「ドア変更なし」→確率1/3 「ドア変更あり」→確率2/3(変更なしの余事象)
となっていました。
これは、ドアごとにあたりの確率が変わっても同じです。
ということで、うまくいってそうですね。
けど、このゲームでドアCを最初に選択できる人ってどれくらいいるんでしょうか?私には無理でしょうね。
満足したので、ここらへんで終わりにしましょう。
FIN
PyQさんで勉強中!





コメント