
くじ引きだけで、いろんな検証ができた。
遊んでいたら、宝くじの厳しさが分かった・・・
記事①:Pythonで当選率10%のくじを10回引く ~確率の悪魔 vs Python ep1 ~
記事②:Pythonで当選率10%のくじを10回引く(完成編)~確率の悪魔 vs Python ep 2~
記事③:Pythonでくじがあたるまで引く ~確率の悪魔 vs Python ep 3~
「10%の確率で当たるくじを、10回引いた時にあたる確率は計算上では、65.13%であるが、本当にそうなるかを検証する」を目標にしてやってきましたが、できたプログラムを拡張して、くじ引きにまつわる、いろいろな確率を検証してきました。
今回は、過去3回の検証でもれていたところと、できたものの集約をやってみましょう!
(2021年3月3日:学習開始12日目、PyQさんで学習中)
前回、幸運をつかむことがいかに難しいかを突きつけられました。
という事で今回は、先日まさかの解散が発表されたDuft Punkさんから、「Get Lucky ft. Pharrell Williams, Nile Rodgers」を聞きながらプログラムを書いていきます。(曲名から公式YouTubeに飛びます。)
まずは、前回の振り返りからやっていきましょう!!
(出来上がったコードをすべてコピペする事で、各自のPCで遊べます。
やり方は「10分でプログラマーになろう ~100000000人をごぼう抜き~」参考にしてください)
1.今までのプログラムの数学的検証
前回、最終的に2つのプログラムを作りました。(参照:確率の悪魔 vs Python ep 3)
①:確率x%で当たるくじを、n回引くとあたりが出る確率は何%か?
②:確率x%で当たるくじを、あたりが出るまで引くには何回引く必要があるか?
①の方は、当たらない確率(1-x/100)をn回繰り返した場合の余事象になるので、このような式で表せます。
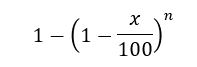
②の方は、期待値計算になります。私には難しいので、まず1例で考えてみます。
例えば、5回目であたる確率は、4回目まではずれて5回目で当たりになりますので、以下の式で書けます。
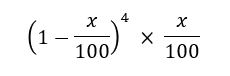
期待値計算になるので、確率に値(上の場合5)をかけたものを足し合わせていけばよいため、最終的に②を表す式は、以下のようになります。(と思います。②の方は自信なし・・)
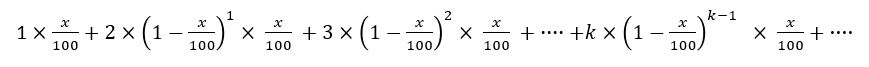
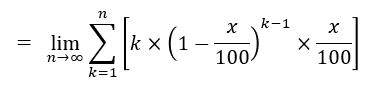
①の方は、計算機を使用すればすぐに確率を出すことができますが、②の方は、数学の勉強をやり直さなければ答えを出すことができません。(積分使いますよね、たしか)
今回、Pythonを使用して試行回数を重ねることで、②の答えを類推することができました。
実際、プログラムで結果を出してから数式を考えているので、数学の知識なしに一定の答えを出したことになります。やはり、プログラムは強力なツールであることがよく分かります。
ただし、「数式の答えとプログラムで試行した結果は異なるものである」という事は、よく認識しておく必要があるようにも思います。
2.改変検証③ ~一定確率以上であたりを出すためには~
ギャンブルをする時(違法賭博ダメ!絶対!)に考えるのは、どこまで突っ込めば、どれくらいの確率であたるのか?裏をかえすと、今回のくじ引きの場合で言うと、「一定の確率で当てるためには、何回引けばよいのか?」という事であると思います。
ちょうど上の①と②を合わせたような考え方です。これをPythonで求めてみたいと思います。
今回は、数式から考えてみましょう。①の式が確率を求めるものでしたが、今回はこの確率が先に決まっていて、引く回数nを求めたいというものなので、下記のようになります。(多分・・・)
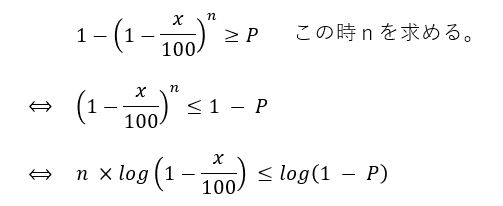
この計算はしませんが、簡単に出せる計算ではありません。
では、プログラムで求めていきましょう。
フローチャートから考えてみましょう。
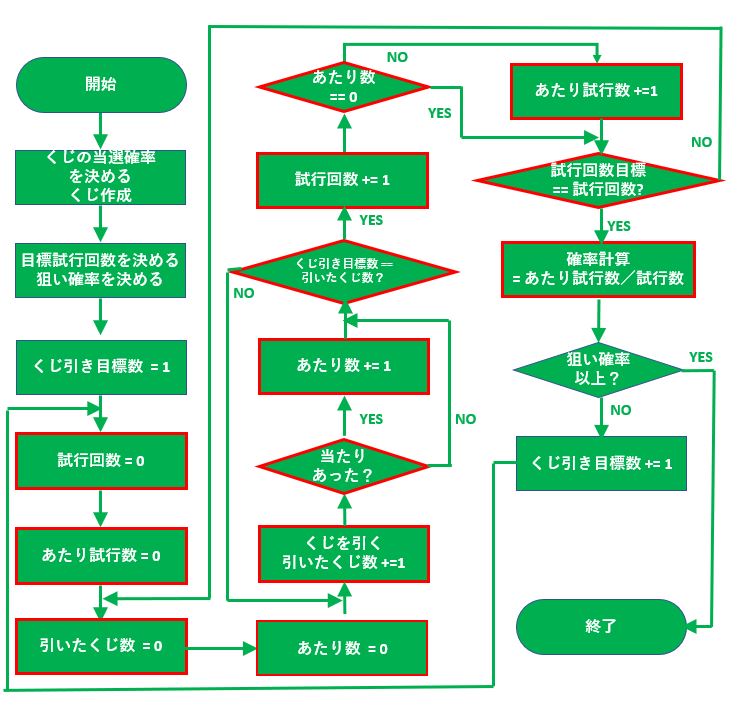
うわー複雑です。やっていることは、
くじ引き回数を最初は1とする
→所定回数試行
→当たる確率を計算
→所定確率以下の場合はくじ引き回数を+1として初めから
という事ですが、フローチャートでは複雑ですね。
所定回数くじ引き、所定試行回数実施、くじ引き回数+1大きく3回ループが「入れ子」状になっているのが複雑な原因ですね。
フローを作って分かったのは、「どのタイミングで値を0にするか?が重要」という事です。
これまでは、どの順番で0にしてもよかったものが、今回はよく考える(というより何度も順番を組み替える)必要がありました。
やはり初心者はいきなりプログラムを書かずにフローチャートから入った方が良さそうです。
ただしフローチャートで赤く囲っているところは、前回作成したものとほぼ変わらないので流用可能です。
では、プログラムを書いていきましょう!!
まずは、import randomですね。
続いて、くじを作るところですが、これも前回のものを流用できます。要は、当選率を入力、くじのあたり何分の1と分数表示してくじ総数を算出、くじを作成という事です。
import random
tousenn = input('当選率は何%?:') #当選率をinput
kuji_num = int(100/float(tousenn)) #くじの数をkuji_num
kuji = range(kuji_num-1) #くじをつくるちなみに今回から説明書き#の書き方を変えました。
説明書きに1行使うと、①どんどん長くなる。②コードをコピーして移動する際に2行分コピーする必要があり失敗すると説明がぐちゃぐちゃになる。というデメリットが見えてきたので、この書き方にしていきます。
続いて、「目標試行回数のインプット」と「狙い確率のインプット」です。この辺りも前回の流用で行けます。その次の「くじ引き目標数=1」も一緒にやってしまいましょう。
prog_target = int(input('試行回数は?:')) #目標試行回数
kakuritsu_target = int(input('狙い確率何%以上?:')) #狙いの確率
kujibiki_target = 1 #くじ引き目標数を初回1に設定次から赤枠のところに入るので、一気に行きましょう。「試行回数=0」~ 「あたり数+= 1」まで行きます。ただし、後々、戻ってくるので注意が必要です。あとで修正は可能ですので、とりあえず上から順に行きます。
prog_num = 0 #試行回数
prog_atari_num = 0 #1あたり試行数
hiku_num = 0 #引いたくじ数
atari_count = 0 #あたり数
your_kuji = random.choice(kuji)
#くじをひく your_kujiが引いたくじ 0ならあたり、×ならはずれ
hiku_num += 1 #引いたくじ数+1
if your_kuji == 0:
atari_count += 1 #あたりがあればあたり数+1
else:
pass続いて、「くじ引き目標数==引いたくじ数?」~「あたり試行数+=1」まで行きましょう。
直前のコードをループさせることになるので、whileを上に持ってきます。
while True: #くじ引き繰り返しのループ
if hiku_num == kujibiki_target:
prog_num += 1 #試行回数+1
break
else:
your_kuji = random.choice(kuji)
~~~~略~~~~
else:
pass
if atari_count == 0:
pass #全滅
else:
prog_atari_num += 1はい、ここまでは書けました。次は、「試行回数目標==試行回数?」と「確率計算」です。
ここでは、試行回数が目標値になっていなければループします。フローチャートに合わせて、引いたくじ数をリセットする前に戻ります。
~~~~略~~~~
prog_atari_num = 0 #1あたり試行数
while True:
if progu_num == prog_target:
prob = 100*(prog_atari_num/prog_target) #確率計算
break
else:
hiku_num = 0 #引いたくじ数
~~~~略~~~~だんだん完成に近づいてきました。
次は、「出てきたあたり確率が、狙いの確率以上になっているかの判定」と「狙い以下の場合、くじ引き目標数を1増やして戻る」というところです。
またwhile構文で繰り返すのですが、ここで戻るのは、「くじ引き目標数=1」と「試行回数=0」の間です。
while True:
if prob < kakuritsu_target: #出てきた確率が狙い確率以下
kujibiki_target += 1
prog_num = 0 #試行回数
prog_atari_num = 0 #あたり試行数
while True:
~~~略~~~
else:
break
print('必要なくじ引き回数:',kujibiki_target,'回')おっと!問題が発生しました。
prob =確率計算はもっと下流で定義していたので、ここで定義しておく必要があります。
もう一つ、probの中身はprog_atari_num/prog_targetですが、prog_atari_numの定義も下に来てしまいます。一方で今記載している箇所で、prog_atari_numはリセットしてループを回したいので、上記の場所にも残しておく必要があります。
という事で、「prog_atari_numは上流で定義」、「probは直前で定義」、「prog_atari_numはリセットする」を考慮して修正しました。また、くじ引数、あたり回数、確率を出力するようにしておきました。
while True:
prob = 100*(prog_atari_num/prog_target) #確率計算
if prob < kakuritsu_target: #出てきた確率が狙い確率以下
print('くじ引き数', kujibiki_target,'あたりが出た回数',prog_atari_num,'確率は', prob, '%')
kujibiki_target += 1
prog_num = 0 #試行回数
prog_atari_num = 0 #1あたり試行数
while True:これで、すべて書けました。今までのを一つにして、動かしてみましょう。
import random
tousenn = input('当選率は何%?:') #当選率をinput
kuji_num = int(100/float(tousenn)) #くじの数をkuji_num
kuji = range(kuji_num-1) #くじをつくる
prog_target = int(input('試行回数は?:')) #目標試行回数
kakuritsu_target = int(input('狙い確率何%以上?:')) #狙いの確率
kujibiki_target = 0 #くじ引き目標数を初回1に設定
prog_atari_num = 0 #1あたり試行数
while True:
prob = 100*(prog_atari_num/prog_target) #確率計算
if prob < kakuritsu_target: #出てきた確率が狙い確率以下
print('くじ引き数', kujibiki_target,'あたりが出た回数',prog_atari_num,'確率は', prob, '%')
kujibiki_target += 1
prog_num = 0 #試行回数
prog_atari_num = 0 #あたり試行数
while True:
if prog_num == prog_target:
break
else:
hiku_num = 0 #引いたくじ数
atari_count = 0 #あたり数
while True: #くじ引き繰り返しのループ
if hiku_num == kujibiki_target:
prog_num += 1 #試行回数+1
break
else:
your_kuji = random.choice(kuji)
#くじをひく your_kujiが引いたくじ 0ならあたり、×ならはずれ
hiku_num += 1 #引いたくじ数+1
if your_kuji == 0:
atari_count += 1 #あたりがあればあたり数+1
else:
pass
if atari_count == 0:
pass #全滅
else:
prog_atari_num += 1
else:
break
print('必要なくじ引き回数:',kujibiki_target,'回')結果が以下です。
当選率は何%?:10
試行回数は?:10000
狙い確率何%以上?:80
くじ引き数 0 あたりが出た回数 0 確率は 0.0 %
くじ引き数 1 あたりが出た回数 1084 確率は 10.84 %
くじ引き数 2 あたりが出た回数 2094 確率は 20.94 %
くじ引き数 3 あたりが出た回数 3040 確率は 30.4 %
くじ引き数 4 あたりが出た回数 3685 確率は 36.85 %
くじ引き数 5 あたりが出た回数 4449 確率は 44.49 %
くじ引き数 6 あたりが出た回数 5088 確率は 50.88 %
くじ引き数 7 あたりが出た回数 5560 確率は 55.60000000000001 %
くじ引き数 8 あたりが出た回数 6127 確率は 61.27 %
くじ引き数 9 あたりが出た回数 6610 確率は 66.10000000000001 %
くじ引き数 10 あたりが出た回数 6902 確率は 69.02000000000001 %
くじ引き数 11 あたりが出た回数 7241 確率は 72.41 %
くじ引き数 12 あたりが出た回数 7592 確率は 75.92 %
くじ引き数 13 あたりが出た回数 7830 確率は 78.3 %
必要なくじ引き回数: 14 回おーーーできましたね。この結果から、10%当選率のくじを80%の確率であてるには14回引く必要があるということがわかりました。
森永チョコボールというお菓子には、金のエンゼル、銀のエンゼルというものがたまについており、金のエンゼルは1つで、銀のエンゼルは5つでおもちゃをもらえます。
そのうち、銀のエンゼルは、どうやら30箱の1つ入っているそうです。
(鳥取の社長日記さんのブログ【1,000箱目】森永チョコボール 金・銀のエンゼルが出る確率を出すで実際に検証しているのを参考にさせていただきました。)
これをもとに、
「銀のエンゼルを90%以上の確率で出すには、何箱のチョコボールを買えばよいか?」
というのをやってみましょう。結果は以下です。
当選率は何%?:3
試行回数は?:10000
狙い確率何%以上?:90
くじ引き数 0 あたりが出た回数 0 確率は 0.0 %
くじ引き数 1 あたりが出た回数 329 確率は 3.29 %
くじ引き数 2 あたりが出た回数 637 確率は 6.370000000000001 %
くじ引き数 3 あたりが出た回数 889 確率は 8.89 %
~~~~~~~~略~~~~~~~~
くじ引き数 29 あたりが出た回数 6048 確率は 60.480000000000004 %
くじ引き数 30 あたりが出た回数 6145 確率は 61.45 %
くじ引き数 31 あたりが出た回数 6241 確率は 62.41 %
くじ引き数 32 あたりが出た回数 6374 確率は 63.739999999999995 %
くじ引き数 33 あたりが出た回数 6482 確率は 64.82 %
くじ引き数 34 あたりが出た回数 6660 確率は 66.60000000000001 %
~~~~~~~~略~~~~~~~~
くじ引き数 68 あたりが出た回数 8872 確率は 88.72 %
くじ引き数 69 あたりが出た回数 8882 確率は 88.82 %
くじ引き数 70 あたりが出た回数 8924 確率は 89.24 %
くじ引き数 71 あたりが出た回数 8996 確率は 89.96 %
必要なくじ引き回数: 72 回という事で、72箱買えば、90%の確率で出せるとの結果です。
これは、「1枚の銀のエンゼルを高確率で出す購入数」になり、逆に言うと、」72箱買って出ない確率は10%以下」という事です。
5枚あつめるのに、72X5の360箱という事ではないです。
30箱あたりでは65%程度になります。実際には、5枚集めるために大量購入するのであれば、結局30箱に1つというところに落ち着きます。
(ところで、一発でうまくいったように書いていますが、実は何度か修正しています。プログラムの中身は問題はなかったのですが、以下の2点で動かなくなりました。
・コードと#説明文の間に全角スペースが入っていた。(半角スペースは問題ないようです。)
・random.choice(kuji)のあとに半角スペースが入っていた。
ここは半角でもNGのようです。importしたものは注意が必要です。)
3.いままでのプログラムを呼び出す「くじ引きマシーン」
長かったくじ引きの検証も最後になりました。
これまでに3つのプログラムを作ってきました。
①:確率x%で当たるくじを、n回引くとあたりが出る確率は何%か?
②:確率x%で当たるくじを、あたりが出るまで引くには何回引く必要があるか?
③:確率x%で当たるくじを、ある確率以上で当てるには何回引く必要があるか?
これらを統合する呼び出しマシーンを作ります。
上のプログラムはそれぞれ、以下の名前で保存しています。
①:kuji_1.py ②:kuji_2.py ③:kuji_1.py
作った.pyのプログラムは、別のプログラムにインポートすることが可能であることが分かりました。やり方はrandomと同じようにimport kuji_1のように呼び出せるようです。
では、やってみましょう!!
print('くじびきマシーン!')
print('何を計算しますか?')
print('1 : くじを複数回引いた場合、あたりが出る確率は?')
print('2 : くじを何回ひけばあたりが出るか?')
print('3 : くじを特定確率以上であてるには、何回ひけばよいか?')
mc_no = input('1, 2, 3から選んでください。やめる場合はそれ以外の値を入れてください : ')
if mc_no == '1':
import kuji_1
elif mc_no == '2':
import kuji_2
elif mc_no == '3':
import kuji_3
else:
passこれは簡単ですね。実際に動かしてみます。上のプログラムはkuji_mc.pyです。
あと、kuji_mc.pyとkuji_1.py以下3つのプログラムは同じフォルダに入っているのが前提です。
C:\Users\ > python kuji_mc.py
くじびきマシーン!
何を計算しますか?
1 : くじを複数回引いた場合、あたりが出る確率は?
2 : くじを何回ひけばあたりが出るか?
3 : くじを特定確率以上であてるには、何回ひけばよいか?
1, 2, 3から選んでください。やめる場合はそれ以外の値を入れてください : 2
当選率は何%?:10
試行回数は?:100
試行回数 100
当たるまでの平均くじ引き数は 7.96 回できてますね。1~3すべてうまく動きました。
ここで分かるのは、いろいろな動きをする.pyファイルを作っておいてインポートすれば、かなり複雑な動きもできるようになるという事です。
これは、非常に重要なテクニックになるような気がしています。
これにて、くじ引きの確率検証は終わりとします。
Fin.
PyQさんで勉強中!





コメント