
10%当選率くじを10回引くと、計算通りだった。
そうなると、いろいろ気になってきた!
記事①:Pythonで当選率10%のくじを10回引く ~確率の悪魔 vs Python ep1 ~
記事②:Pythonで当選率10%のくじを10回引く(完成編)~確率の悪魔 vs Python ep 2~
前回、前々回と、「10%の確率で当たるくじを、10回引いた時にあたる確率は計算上では、65.13%であるが、本当にそうなるかを検証する」という事をpythonでやってきました。
結論としては、確かにそのようになりました。
今回は、過去2回で作ってきたプログラムを改変して、ほかの確率を検証していきます!
(2021年2月28日:学習開始9日目、PyQさんで学習中!)
今回はThe Rolling Stonesさんで「ダイスを転がせ(Tumbling Dice)」とともにやっていきます。例によって、曲名からYouTube公式動画に飛びます。
では、行きましょう!!!
(出来上がったコードをすべてコピペする事で、各自のPCで遊べます。
やり方は「10分でプログラマーになろう ~100000000人をごぼう抜き~」参考にしてください)
1.改変検証① ~くじの当選率が変わるとどうなるか?~
まずは、前回の最後に作ったコードを振り返ります。
import random
#10回判定プログラム試行数
prog_num = 0
#10回判定プログラムあたり回数
prog_atari_num = 0
#引いた回数
hiku_num = 0
#あたり回数
atari_count = 0
#くじをつくる
kuji = ['〇', '×1', '×2','×3','×4','×5','×6','×7','×8','×9',]
while True:
#10回判定プログラム試行数が10回になるまで繰り返す。
if prog_num == 10:
break
else:
while True:
if hiku_num == 10:
prog_num += 1
break
else:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
#〇ならあたり、×ならはずれ
#print(your_kuji)
hiku_num += 1
if your_kuji == '〇':
#print('あたり')
atari_count += 1
else:
#print('はずれ')
pass
if atari_count == 0:
#print('全滅!')
pass
else:
#print('あたりあった!')
prog_atari_num += 1
hiku_num = 0
atari_count = 0
print('試行回数',prog_num)
print('あたりが出た回数',prog_atari_num)
#確率計算
prob = 100*(prog_atari_num/prog_num)
print('確率は', prob, '%')これを改変していきましょう。
前回は、くじの当選率10%、引く回数を10回としましたが、これが当選率1%、引く回数100回とした場合どうなるでしょうか?
確率で計算してみましょう。
>>> 1-(99/100)**100
0.633967658726770963.4%となりました。
なんと、当選率10%、引く回数10回の場合とほぼ変わりません。
元のプログラムでは、kuji = [‘〇’, ‘×1’, ‘×2′,’×3′,’×4′,’×5′,’×6′,’×7′,’×8′,’×9’,]と定義しています。
Xを99個書けば、同じようにできますが、とても大変です。
また当選率0.01%とかになると対応できません。
そこで、kijiを0~99の数字のリストと考えて、0が出たらあたりという事にしてはどうでしょうか?コードで表現してみましょう。
kuji = range(99)次は当たりの定義を変えましょう。
これまでは〇をあたりとしていましたが、0(ゼロ)をあたりとみなします。
if your_kuji == 0:
#print('あたり')
atari_count += 1
else:
#print('はずれ')
pass続いて、
引く回数を100(if hiku_num == 100)
試行回数をいったん(if prog_num == 10)としましょう。
また、検証のために1試行ごとの「あたり」「全滅」もprintで出すことにします。
import random
#10回判定プログラム試行数
prog_num = 0
#10回判定プログラムあたり回数
prog_atari_num = 0
#引いた回数
hiku_num = 0
#あたり回数
atari_count = 0
#くじをつくる
kuji = range(99)
while True:
#10回判定プログラム試行数が10回になるまで繰り返す。
if prog_num == 10:
break
else:
while True:
if hiku_num == 100:
prog_num += 1
break
else:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
#0ならあたり、×ならはずれ
#print(your_kuji)
hiku_num += 1
if your_kuji == 0:
#print('あたり')
atari_count += 1
else:
#print('はずれ')
pass
if atari_count == 0:
print('全滅!')
pass
else:
print('あたりあった!')
prog_atari_num += 1
hiku_num = 0
atari_count = 0
print('試行回数',prog_num)
print('あたりが出た回数',prog_atari_num)
#確率計算
prob = 100*(prog_atari_num/prog_num)
print('確率は', prob, '%')結果は以下です。
あたりあった!
あたりあった!
あたりあった!
あたりあった!
あたりあった!
全滅!
あたりあった!
あたりあった!
あたりあった!
あたりあった!
試行回数 10
あたりが出た回数 9
確率は 90.0 %確率が高すぎるような気がします・・・コードが間違っているのでしょうか?
試行回数が低すぎるのでしょうか?
「あたり」「全滅」のprintを消して、試行回数を1000にしてみました。
試行回数 1000
あたりが出た回数 650
確率は 65.0 %結果は65%!!おお、確率計算の結果と同じようになりました。
ところで、当選率をX%、引く回数をY回、試行回数をnとして毎回入れるようにできれば、いろいろ検証しやすいのではないでしょうか?
input()を使えばよいと思います。
tousenn = input('当選率は何%?:')
#くじの数をkuji_num
kuji_num = int(100/float(tousenn))
#くじをつくる
kuji = range(kuji_num-1)
#くじ引き回数
kujibiki_target = int(input('くじ引き回数は?:'))
#試行回数
prog_target = int(input('試行回数は?:'))ちなみにここに至るまでに、いくつか修正しました。
・inputで入れた値は文字列になるので、intで整数にする必要があります。
・当選率は小数もあり得るのでfloatで小数にしています。
・kuji_num = 100/float(tousenn)とすると小数型になります。
次のrangeでエラーになるので、kuji_numをintで整数にする必要があります。
・inputに数字以外を入れる、当選率に50以上を入れる、くじ引き数と試行回数に1未満をいれるとエラーになります。ここはキチンと修正するとかなり長くなりそうです。おかしな値を入れるとエラーでストップ、正しい値で先に進むので修正はパスします。
続いて、inputで入れた数字を終了条件に反映させます。
if prog_num == prog_target:
~~~略~~~
if hiku_num == kujibiki_target:できました。次がコード全文です。
import random
#10回判定プログラム試行数
prog_num = 0
#10回判定プログラムあたり回数
prog_atari_num = 0
#引いた回数
hiku_num = 0
#あたり回数
atari_count = 0
#当選率をinput
tousenn = input('当選率は何%?:')
#くじの数をkuji_num
kuji_num = int(100/float(tousenn))
#くじをつくる
kuji = range(kuji_num-1)
#くじ引き回数
kujibiki_target = int(input('くじ引き回数は?:'))
#試行回数
prog_target = int(input('試行回数は?:'))
while True:
#10回判定プログラム試行数が10回になるまで繰り返す。
if prog_num == prog_target:
break
else:
while True:
if hiku_num == kujibiki_target:
prog_num += 1
break
else:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
#0ならあたり、×ならはずれ
#print(your_kuji)
hiku_num += 1
if your_kuji == 0:
#print('あたり')
atari_count += 1
else:
#print('はずれ')
pass
if atari_count == 0:
#print('全滅!')
pass
else:
#print('あたりあった!')
prog_atari_num += 1
hiku_num = 0
atari_count = 0
print('試行回数',prog_num)
print('あたりが出た回数',prog_atari_num)
#確率計算
prob = 100*(prog_atari_num/prog_num)
print('確率は', prob, '%')プログラムの結果が次になります。
当選率0.1%、引く回数1000回、試行回数1000回にしてみました。
当選率は何%?:0.1
くじ引き回数は?:1000
試行回数は?:1000
試行回数 1000
あたりが出た回数 630
確率は 63.0 %ちなみに確率計算では以下のようになり、63.2%です。
>>> 1-(999/1000)**1000
0.6323045752290363だいたい合ってますね。
2.改変検証② ~じゃあ何回引けば当たるのか?~
これまでの検証で、10回引くと65%の確率で当たると分かりました。
でも、実際の場面で知りたいのは、「じゃあ何回ひけばいいのか?」ということですよね?
当たるまでの回数の平均回数を出してみたいと思います。
また、改変検証①でやった当選率と試行回数のinputはそのまま採用しようと思います。
・くじの当選率は10%というのはそのまま行きます。(inputで10を入れる)
・これまでは引く回数は10回固定でしたが、今回は当たるまで引きます。
・「当たるまで引く」というのをさらに繰り返し、平均回数を算出します。
まず、11行目のくじの定義はそのままでOKですね。
次に、18行目、1週のサイクルの終了条件ですが、これは、「あたりが出たら」という事になりますね。試行回数を増やすのはそのままです。
あと、くじをひくタイミングも変えないといけないですね。
#~~~~略~~~~
else:
else:
while True:
if your kuji == 0
#if hiku_num == 10:
prog_num += 1
break
#~~~~略~~~~や、やばい・・・簡単に考えてましたが、結構な改変が必要っぽいです。
フローチャートから考え直してみます。
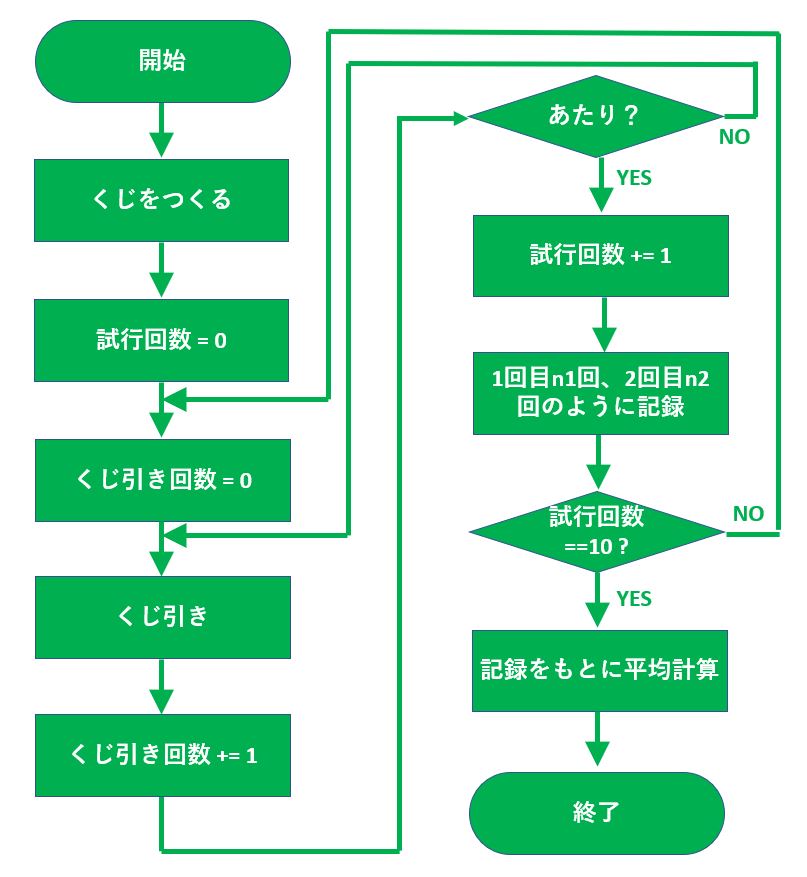
なるほど、これは一筋縄にはいかないです。ひとつずつ見直しましょう。
元のコードでいらなさそうなのが、「あたり回数=atari_count」「10回判定プログラムあたり回数=prog_atari_num(常に1になるはずです。)」。これらを消します。
特に、引いた回数を順番に記録していくのが難しそうです。
リスト型のデータ[n1,n2,・・・]と記録していけば良さそうに思います。
続いて、「くじ引き→くじ引き回数+1→あたり判定のループ」と「あたった場合に試行回数を1増やしてループを抜ける」というところを作ります。
while True:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
hiku_num += 1
if your_kuji == 0:
prog_num += 1
break
else:
passこれでよいと思います。
では、「試行ごとにあたるまで引いた回数を記録」を考えます。少し難しいです。
イメージとしてはリスト型のデータ[n1,n2,・・・]と記録していけば良さそうに思います。
まず上のほうで、試行回数リストを定義し、 あたりが出たらくじ引き回数をリストに加えればよいのではないでしょうか?
ちょっとコードで書いてみましょう。
#引いた回数リスト
num_list = []
~~~略~~~
if your_kuji == 0:
prog_num += 1
num_list.append(hiku_num)
breakその次は、「試行回数が10回かどうかを判定し、10回未満で繰り返し、10回であれば抜ける」というところを考えます。ここは、元のプログラムと同じ考えで行けますので、ここでは省略します。
ここまでをまとめてプログラムにして、printで出力してみます。
コードは以下です。元のものとかなり変わってしまいました。
import random
#プログラム試行数
prog_num = 0
#引いた回数
hiku_num = 0
#当選率をinput
tousenn = input('当選率は何%?:')
#くじの数をkuji_num
kuji_num = int(100/float(tousenn))
#くじをつくる
kuji = range(kuji_num-1)
#試行回数
prog_target = int(input('試行回数は?:'))
#引いた回数リスト
num_list = []
while True:
#引いた回数
hiku_num = 0
#10回判定プログラム試行数が10回になるまで繰り返す。
if prog_num == prog_target:
break
else:
while True:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
hiku_num += 1
if your_kuji == 0:
prog_num += 1
num_list.append(hiku_num)
break
else:
pass
print('試行回数',prog_num)
print(num_list)出力結果は以下です。
当選率は何%?:10
試行回数は?:10
試行回数 10
[19, 5, 3, 1, 5, 25, 8, 11, 4, 4]どうやら行けてそうです。print(num_list)は消しておきます。
次は、ここから、平均くじ引き回数の算出です。
listに入っている数字をすべて足して、試行回数で割れば良いのですね。
listのひとつずつ処理していくのはforを使うのでした。
#確率計算
#引いた数の合計
sum_hiki = 0
for hiki in num_list:
sum_hiki += hiki
ave_hiki = sum_hiki/prog_numこれまでのものを合算して、最後に平均くじ引き回数をprintします。
import random
#プログラム試行数
prog_num = 0
#引いた回数
hiku_num = 0
#当選率をinput
tousenn = input('当選率は何%?:')
#くじの数をkuji_num
kuji_num = int(100/float(tousenn))
#くじをつくる
kuji = range(kuji_num-1)
#試行回数
prog_target = int(input('試行回数は?:'))
#引いた回数リスト
num_list = []
while True:
#引いた回数
hiku_num = 0
#10回判定プログラム試行数が10回になるまで繰り返す。
if prog_num == prog_target:
break
else:
while True:
#くじをひく your_kujiが引いたくじ
your_kuji = random.choice(kuji)
hiku_num += 1
if your_kuji == 0:
prog_num += 1
num_list.append(hiku_num)
break
else:
pass
print('試行回数',prog_num)
#確率計算
#引いた数の合計
sum_hiki = 0
for hiki in num_list:
sum_hiki += hiki
ave_hiki = sum_hiki/prog_num
print('当たるまでの平均くじ引き数は', ave_hiki, '回')では出力してみましょう。当選率は10%、試行回数は100とします。
当選率は何%?:10
試行回数は?:100
試行回数 100
当たるまでの平均くじ引き数は 8.96 回できました。
平均的には9回引けば当たるという事ですね。
くじのあたりの確率10%に近い数字になりますね。
10回以内であたる確率は65%くらい、つまり半数以上という事を考えると妥当な気がします。
ちなみに、宝くじの1等があたる確率は、2000万分の1(=0.000005%)だそうです。
これを入れてみると、試行回数が1でもプログラムが数分まっても終わらなくなってしまいました
(※ 後日、再トライしました。50回試行で平均くじ引き数は 20596092.84 回、約2060万回!!!引く必要があります。
1枚300円として、61億8000万円分!!!。あまり書くと、宝くじの人に怒られそうなので止めときます。ちなみに50回試行で私のPCでは20分くらいかかりました。)
<重要>大きすぎる数字を入れると、計算に時間がかかり終わらなくなります。
実行したプログラムを強制終了させるには、
Windowsの場合:Ctrlを押しながらcを押す
Macの場合:control を押しながら cを押す
宝くじの2等やジャンボミニ宝くじの1等があたる確率は、200万分の1(=0.00005%)だそうです。50回試行とすると数分かかって以下の結果になりました。
当選率は何%?:0.00005
試行回数は?:50
試行回数 50
当たるまでの平均くじ引き数は 2189802.86 回確率の低さに対して試行回数が足りていないとは思いますが、2等をあてるのでも219万回引く必要があるという結果です。お、恐ろしい・・・
今回は、前回つくったプログラムをもとに新たなプログラムを2つ作成して遊んでみました。
次回は、今回の2つのプログラムを組み合わせて、集大成のプログラムをつくってみたいと思っています。
To Be Continued : 確率の悪魔 vs Python episode 4
PyQさんで勉強中!





コメント